Question

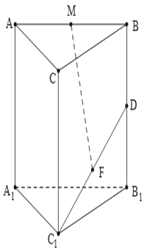
【題目】三棱柱中，平面，為正三角形，為中點，為線段的中點，為中點．

（1）求證：面；

（2）求證：．

Answer 1

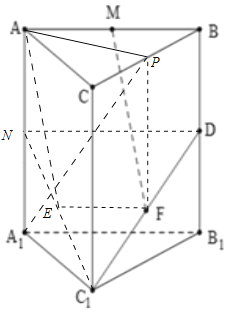
【答案】（1）證明見解析（2）證明見解析

【解析】

（1）取中點，連結，，取中點，連結，，由已知可證，又，可證四邊形為平行四邊形，可證，利用線面平行的判定定理即可證明面．

（2）設中點為，連接，，可證，，可證，可證，又正三角形中，為中點，可證，利用線面垂直的判定定理可證平面，根據線面垂直的性質定理可證．

證明：（1）取中點，連結，，

取中點，連結，，

，，

四邊形為平行四邊形，

，，

，，

又，

四邊形為平行四邊形，

，

面，面，

面．

（2）設中點為，連接，，

三棱柱中，，為中點，

四邊形為梯形，

又為中點，為線段的中點，

，

三棱柱中，，

，

平面，

三棱柱中，平面，且平面，

①

正三角形中，為中點，則②，

由①②及，得平面，

．