
【題目】如圖,三棱柱![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
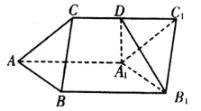
(1)求證:![]() ;
;
(2)若![]() ,直線
,直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,![]() 為
為![]() 的中點,求二面角
的中點,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)![]()
【解析】
(1)過點C作CO⊥AA1,則CO⊥平面AA1B1B,CO⊥OB,推導出Rt△AOC≌Rt△BOC,從而AA1⊥OB,再由AA1⊥CO,得AA1⊥平面BOC,由此能證明AA1⊥BC.
(2)以O為坐標原點,OA,OB,OC所在直線分別為x,y,z軸,建立空間直角坐標系,利用向量法能求出二面角B1﹣A1D﹣C1的余弦值.
(1)過點![]() 作
作![]() ,垂足為
,垂足為![]() ,
,
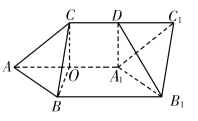
因為平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() ,
,
又因為![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() ,
,
因為![]() ,所以
,所以![]() ,
,
又因為![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() .
.
(2)以![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() ,
,
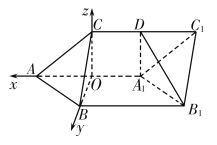
因為![]() 平面
平面![]() ,
,
所以![]() 是直線
是直線![]() 與平面
與平面![]() 所成角,
所成角,
故![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則
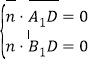 ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ,
,
因為![]() 平面
平面![]() ,
,
所以![]() 為平面
為平面![]() 的一條法向量,
的一條法向量,
![]() ,
,
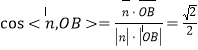 ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)若函數在區間![]() 上存在零點,求實數p的取值范圍;
上存在零點,求實數p的取值范圍;
(2)問是否存在常數![]() ,使得當
,使得當![]() 時,
時,![]() 的值域為區間D,且D的長度為
的值域為區間D,且D的長度為![]() .
.
(注:區間![]()
![]() 的長度為
的長度為![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解用戶對其產品的滿意度,從A、B兩地區分別隨機調查了20個用戶,得到用戶對產品的滿意度評分如下:
A地區: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地區: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根據兩組數據完成兩地區用戶滿意度評分的莖葉圖,并通過莖葉圖比較兩地區滿意度的平均值及分散程度(不要求算出具體值,給出結論即可):

(Ⅱ)根據用戶滿意度評分,將用戶的滿意度從低到高分為三個等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
記事件C:“A地區用戶的滿意度等級高于B地區用戶的滿意度等級”,假設兩地區用戶的評價結果相互獨立,根據所給數據,以事件發生的頻率作為相應事件發生的概率,求C的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是橢圓
是橢圓![]() 上任一點,點
上任一點,點![]() 到直線
到直線![]() :
:![]() 的距離為
的距離為![]() ,到點
,到點![]() 的距離為
的距離為![]() ,且
,且![]() ,若直線
,若直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 軸上方),且
軸上方),且![]() .
.
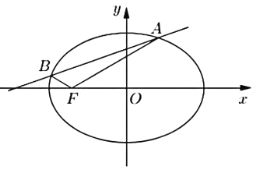
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)當![]() 為橢圓與
為橢圓與![]() 軸正半軸的交點時,求直線
軸正半軸的交點時,求直線![]() 的方程;
的方程;
(3)對于動直線![]() ,是否存在一個定點,無論
,是否存在一個定點,無論![]() 如何變化,直線
如何變化,直線![]() 總經過此定點?若存在,求出定點的坐標,若不存在,請說明理由.
總經過此定點?若存在,求出定點的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦點到短軸的端點的距離為
的焦點到短軸的端點的距離為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,過點
兩點,過點![]() 作平行于
作平行于![]() 軸的直線
軸的直線![]() ,交直線
,交直線![]() 于點
于點![]() ,求證:直線
,求證:直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 上一點,經過點
上一點,經過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 、
、![]() 兩點(不同于點
兩點(不同于點![]() ),直線
),直線![]() 、
、![]() 分別交直線
分別交直線![]() 于點
于點![]() 、
、![]() .
.
(1)求拋物線方程及其焦點坐標;
(2)求證:以![]() 為直徑的圓恰好經過原點.
為直徑的圓恰好經過原點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中所有正確的序號是_________
①兩直線的傾斜角相等,則斜率必相等;
②若動點![]() 到定點
到定點![]() 和定直線
和定直線![]() 的距離相等,則動點
的距離相等,則動點![]() 的軌跡是拋物線;
的軌跡是拋物線;
③已知![]() 、
、![]() 是橢圓
是橢圓![]() 的兩個焦點,過點
的兩個焦點,過點![]() 的直線與橢圓交于
的直線與橢圓交于![]() 、
、![]() 兩點,則
兩點,則![]() 的周長為
的周長為![]() ;
;
④曲線的參數方程為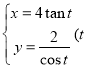 為參數
為參數![]() ,則它表示雙曲線且漸近線方程為
,則它表示雙曲線且漸近線方程為![]() ;
;
⑤已知正方形![]() ,則以
,則以![]() 、
、![]() 為焦點,且過
為焦點,且過![]() 、
、![]() 兩點的橢圓的離心率為
兩點的橢圓的離心率為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若集合![]() 具有以下性質:(1)
具有以下性質:(1)![]() 且
且![]() ;(2)若
;(2)若![]() ,
,![]() ,則
,則![]() ,且當
,且當![]() 時,
時,![]() ,則稱集合
,則稱集合![]() 為“閉集”.
為“閉集”.
(1)試判斷集合![]() 是否為“閉集”,請說明理由;
是否為“閉集”,請說明理由;
(2)設集合![]() 是“閉集”,求證:若
是“閉集”,求證:若![]() ,
,![]() ,則
,則![]() ;
;
(3)若集合![]() 是一個“閉集”,試判斷命題“若
是一個“閉集”,試判斷命題“若![]() ,
,![]() ,則
,則![]() ”的真假,并說明理由.
”的真假,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com