
【題目】某中學從甲乙兩個教師所教班級的學生中隨機抽取100人,每人分別對兩個教師進行評分,滿分均為100分,整理評分數據,將分數以10為組距分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .得到甲教師的頻率分布直方圖,和乙教師的頻數分布表:
.得到甲教師的頻率分布直方圖,和乙教師的頻數分布表:
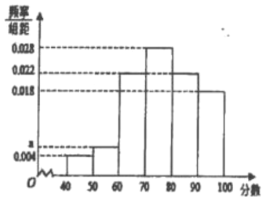
乙教師分數頻數分布表 | |
分數區間 | 頻數 |
| 3 |
| 3 |
| 15 |
| 19 |
| 35 |
| 25 |
(1)在抽樣的100人中,求對甲教師的評分低于70分的人數;
(2)從對乙教師的評分在![]() 范圍內的人中隨機選出2人,求2人評分均在
范圍內的人中隨機選出2人,求2人評分均在![]() 范圍內的概率;
范圍內的概率;
(3)如果該校以學生對老師評分的平均數是否大于80分作為衡量一個教師是否可評為該年度該校優秀教師的標準,則甲、乙兩個教師中哪一個可評為年度該校優秀教師?(精確到0.1)
【答案】(1)![]() 人;(2)
人;(2)![]() ;(3)乙可評為年度該校優秀教師
;(3)乙可評為年度該校優秀教師
【解析】
(1)根據頻率分布直方圖求出70分以上的頻率,總頻率之和為![]() 可得70分以下的頻率,由頻率
可得70分以下的頻率,由頻率![]() 即可求解.
即可求解.
(2)根據頻數分布表![]() 有3人,
有3人,![]() 有3人,分別進行標記,利用列舉法求出隨機選出2人的基本事件個數,然后再求出評分均在
有3人,分別進行標記,利用列舉法求出隨機選出2人的基本事件個數,然后再求出評分均在![]() 范圍內的基本事件個數,根據古典概型的概率計算公式即可求解.
范圍內的基本事件個數,根據古典概型的概率計算公式即可求解.
(3)利用平均數![]() 小矩形的面積
小矩形的面積![]() 小矩形底邊中點橫坐標之和,求出甲的平均分,再利用平均數的公式求出乙的平均分即可得出結果.
小矩形底邊中點橫坐標之和,求出甲的平均分,再利用平均數的公式求出乙的平均分即可得出結果.
(1)由頻率分布直方圖可知,70分以上的頻率為![]() ,
,
70分以下的頻率為![]() ,
,
所以對甲教師的評分低于70分的人數:![]() .
.
(2)由頻數分布表![]() 有3人,
有3人,![]() 有3人,
有3人,
記![]() 的3人為A、B、C,
的3人為A、B、C,![]() 的3人為
的3人為![]() 、
、![]() 、
、![]() ,
,
隨機選出2人:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,共
,共![]() 種;
種;
評分均在![]() 的抽取方法:
的抽取方法:![]() ,
, ![]() ,
,![]() ,共3種;
,共3種;
所以2人評分均在![]() 范圍內的概率
范圍內的概率![]() .
.
(3)由頻率分布直方圖可得![]() 的頻率為:
的頻率為:
![]()
甲教師的平均數為:
![]()
![]() ,
,
乙教師的平均數為:
![]() ,
,
由于乙教師的平均數大于80分,故乙可評為年度該校優秀教師.


科目:高中數學 來源: 題型:
【題目】從盛滿2升純酒精的容器里倒出1升純酒精,然后填滿水,再倒出1升混合溶液后又用水填滿,以此繼續下去,則至少應倒 次后才能使純酒精體積與總溶液的體積之比低于10%.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() ,
,![]() ,拋物線
,拋物線![]() 的焦點
的焦點![]() 為線段
為線段![]() 中點.
中點.
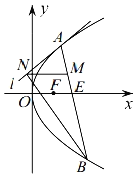
(1)求拋物線![]() 的方程;
的方程;
(2)過點![]() 的直線交拋物線
的直線交拋物線![]() 于
于![]() 兩點,
兩點,![]() ,過點
,過點![]() 作拋物線
作拋物線![]() 的切線
的切線![]() ,
,![]() 為切線
為切線![]() 上的點,且
上的點,且![]() 軸,求
軸,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形ABCD為平行四邊形,且
中,四邊形ABCD為平行四邊形,且![]() ,
,![]() ,
,![]() 平面PAC.
平面PAC.

(1)求證:![]() 平面
平面![]() ;
;
(2)若異面直線PC與AD所成的角為30°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019冠狀病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠狀病毒(2019-nCoV)引發的疾病,目前全球感染者以百萬計,我國在黨中央、國務院、中央軍委的堅強領導下,已經率先控制住疫情,但目前疫情防控形勢依然嚴峻,湖北省中小學依然延期開學,所有學生按照停課不停學的要求,居家學習.小李同學在居家學習期間,從網上購買了一套高考數學沖刺模擬試卷,快遞員計劃在下午4:00~5:00之間送貨到小區門口的快遞柜中,小李同學父親參加防疫志愿服務,按規定,他換班回家的時間在下午4:30~5:00,則小李父親收到試卷無需等待的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體![]() 的棱長為1,P是空間中任意一點,下列正確命題的個數是( )
的棱長為1,P是空間中任意一點,下列正確命題的個數是( )
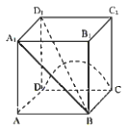
①若P為棱![]() 中點,則異面直線AP與CD所成角的正切值為
中點,則異面直線AP與CD所成角的正切值為![]() ;
;
②若P在線段![]() 上運動,則
上運動,則![]() 的最小值為
的最小值為![]() ;
;
③若P在半圓弧CD上運動,當三棱錐![]() 的體積最大時,三棱錐
的體積最大時,三棱錐![]() 外接球的表面積為
外接球的表面積為![]() ;
;
④若過點P的平面![]() 與正方體每條棱所成角相等,則
與正方體每條棱所成角相等,則![]() 截此正方體所得截面面積的最大值為
截此正方體所得截面面積的最大值為![]()
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的方程為
的方程為![]() ,且直線
,且直線![]() 與以原點為圓心,橢圓
與以原點為圓心,橢圓![]() 短軸長為直徑的圓相切.
短軸長為直徑的圓相切.
(1)求![]() 的值;
的值;
(2)若橢圓![]() 左右頂點分別為
左右頂點分別為![]() ,過點
,過點![]() 作直線
作直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 位于第一象限,
位于第一象限,![]() 在線段
在線段![]() 上.
上.
①若![]() 和
和![]() 的面積分別為
的面積分別為![]() ,問是否存在這樣的直線
,問是否存在這樣的直線![]() 使得
使得![]() ?請說明理由;
?請說明理由;
②直線![]() 與直線
與直線![]() 交于點
交于點![]() ,連結
,連結![]() ,記直線
,記直線![]() 的斜率分別為
的斜率分別為![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現給出三個條件:①函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;②函數
對稱;②函數![]() 的圖象關于點
的圖象關于點![]() 對稱;③函數
對稱;③函數![]() 的圖象上相鄰兩個最高點的距離為
的圖象上相鄰兩個最高點的距離為![]() .從中選出兩個條件補充在下面的問題中,并以此為依據求解問題.
.從中選出兩個條件補充在下面的問題中,并以此為依據求解問題.
已知函數![]() (
(![]() ,
,![]() ),_____,_____.求函數
),_____,_____.求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com