
【題目】已知![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若函數有兩個極值點![]() 和
和![]() ,
,![]() 求證:b<2a
求證:b<2a
【答案】(1)(![]() ,1)是減區間,(0,
,1)是減區間,(0,![]() )和(1,+∞)是增區間;(2)詳見解析
)和(1,+∞)是增區間;(2)詳見解析
【解析】
試題分析:(1)將![]() 代入函數式,通過函數導數的正負得到函數的增減區間;(2)由題意可知
代入函數式,通過函數導數的正負得到函數的增減區間;(2)由題意可知![]() 是方程
是方程![]() 的根,依據根的分布規律可得
的根,依據根的分布規律可得![]() 的不等式,從而得到
的不等式,從而得到![]()
試題解析:(1)f‘(x)=2x-3+![]() =
=![]() (x>0), 2分
(x>0), 2分
由f'(x)=0得x=![]() 或x=1,.∴當x>1或0<x<
或x=1,.∴當x>1或0<x<![]() 時,f'(x)>0,
時,f'(x)>0,
當![]() <x<1時f'(x)<0, 4分
<x<1時f'(x)<0, 4分
∴(![]() ,1)是函數f(x)的減區間,(0,
,1)是函數f(x)的減區間,(0,![]() )和(1,+∞)是f(x)的增區間;..5分
)和(1,+∞)是f(x)的增區間;..5分
(2)∵函數f(x)有兩個極值點x1,x2,∴f(x)=0在(0,+∞)有兩個不同的解x1,x2,
.∵f(x)=ax+(b-1)+![]() =
=![]() , 6分
, 6分
∴x1,x2是ax2+(b-1)x+1=0在(0,+∞)內的兩個不同解,
設h(x)=ax2+(b-1)x+1,則該函數有兩個零點x1,x2,
∵0<x1<2<x2<4,∴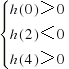 即
即![]() , 9分
, 9分
∴![]() -4a<b<
-4a<b<![]() -2a,即
-2a,即![]() -4a<
-4a<![]() -2a得a>
-2a得a>![]() , 11分
, 11分
∴b<![]() -2a<4a-2a=2a,∴b<2a得證;. 12分
-2a<4a-2a=2a,∴b<2a得證;. 12分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知等比數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() 且
且![]() 為等差數列
為等差數列![]() 的前三項.
的前三項.
(1)求![]() 與數列
與數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 的前
的前![]() 項和
項和![]() ,試問是否存在正整數
,試問是否存在正整數![]() ,對任意的
,對任意的![]() 使得
使得![]() ?若存在請求出
?若存在請求出![]() 的最大值,若不存在請說明理由.
的最大值,若不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面是邊長為
的底面是邊長為![]() 的正方形,
的正方形, ![]() 底面
底面![]() ,
, ![]() 分別為
分別為![]() 的中點.
的中點.
(Ⅰ)求證: ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,試問在線段
,試問在線段![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角 ![]() 的余弦值為
的余弦值為![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用數學歸納法證明當n∈N*時,1+2+22+…+25n-1是31的倍數時,當n=1時原式為( )
A. 1 B. 1+2
C. 1+2+3+4 D. 1+2+22+23+24
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車公司為了考查某![]() 店的服務態度,對到店維修保養的客戶進行回訪調查,每個用戶在到此店或保養后可以對該店進行打分,最高分為10分.上個月公司對該
店的服務態度,對到店維修保養的客戶進行回訪調查,每個用戶在到此店或保養后可以對該店進行打分,最高分為10分.上個月公司對該![]() 店的100位到店維修保養的客戶進行了調查,將打分的客戶按所打分值分成以下幾組:第一組
店的100位到店維修保養的客戶進行了調查,將打分的客戶按所打分值分成以下幾組:第一組![]() ,第二組
,第二組![]() ,第三組
,第三組![]() ,第四組
,第四組![]() a,第五組
a,第五組![]() ,得到頻率分布直方圖如圖所示.
,得到頻率分布直方圖如圖所示.
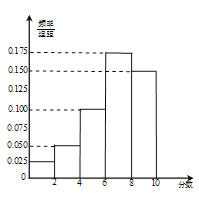
(1)求所打分值在![]() 的客戶的人數;
的客戶的人數;
(2)該公司在第二、三組客戶中按分層抽樣的方法抽取6名客戶進行深入調查,之后將從這6人中隨機抽取2人進行物質獎勵,求得到獎勵的人來自不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的四個頂點分別為
的四個頂點分別為![]() ,左右焦點分別為
,左右焦點分別為![]() ,若圓
,若圓![]() :
:![]() 上有且只有一個點
上有且只有一個點![]() 滿足
滿足![]() .
.
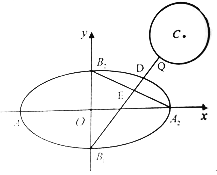
(1)求圓![]() 的半徑
的半徑![]() ;
;
(2)若點![]() 為圓
為圓![]() 上的一個動點,直線
上的一個動點,直線![]() 交橢圓于點
交橢圓于點![]() ,交直線
,交直線![]() 于點
于點![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com