Question

【題目】如圖所示，某班一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損，其中，頻率分布直方圖的分組區間分別為[50，60），[60，70），[70，80），[80，90），[90，100]，據此解答如下問題．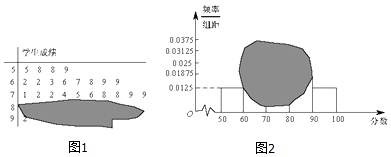
（Ⅰ）求全班人數及分數在[80，100]之間的頻率；
（Ⅱ）現從分數在[80，100]之間的試卷中任取 3 份分析學生情況，設抽取的試卷分數在[90，100]的份數為X，求X的分布列和數學望期．

Answer 1

【答案】解：（Ⅰ）由莖葉圖知分數在[50，60）的人數為4人；[60，70）的人數為8人；[70，80）的人數為10人． ∴總人數為
∴分數在[80，100）人數為32﹣4﹣8﹣10=10人，∴頻率為
（Ⅱ）[80，90）的人數為6人；分數在[90，100）的人數為4人X的取值可能為0，1，2，3．
， ，
， ．
∴分布列為

X	0	1	2	3
P

E（X）=0+ =
【解析】（I）利用莖葉圖的性質、頻率的計算公式即可得出．（II）[80，90）的人數為6人；分數在[90，100）的人數為4人X的取值可能為0，1，2，3．再利用超幾何分布列的概率計算公式及其數學期望計算公式即可得出．
【考點精析】根據題目的已知條件，利用離散型隨機變量及其分布列的相關知識可以得到問題的答案，需要掌握在射擊、產品檢驗等例子中，對于隨機變量X可能取的值，我們可以按一定次序一一列出，這樣的隨機變量叫做離散型隨機變量．離散型隨機變量的分布列：一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn，X取每一個值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，則稱表為離散型隨機變量X 的概率分布，簡稱分布列．