
【題目】已知函數  ,若m<n,且f(m)=f(n),則n﹣m的取值范圍是( )
,若m<n,且f(m)=f(n),則n﹣m的取值范圍是( )
A.[3﹣2ln2,2)
B.[3﹣2ln2,2]
C.[e﹣1,2]
D.[e﹣1,2)
【答案】A
【解析】解:作出函數f(x)的圖象如圖:
若m<n,且f(m)=f(n),
則當ln(x+1)=1時,得x+1=e,即x=e﹣1,
則滿足0<n≤e﹣1,﹣2<m≤0,
則ln(n+1)= ![]() m+1,即m=2ln(n+1)﹣2,
m+1,即m=2ln(n+1)﹣2,
則n﹣m=n+2﹣2ln(n+1),
設h(n)=n+2﹣2ln(n+1),0<n≤e﹣1
則h′(n)=1﹣ ![]() =
= ![]() =
= ![]() ,
,
當h′(x)>0得1<n≤e﹣1,
當h′(x)<0得0<n<1,
即當n=1時,函數h(n)取得最小值h(1)=1+2﹣2ln2=3﹣2ln2,
當n=0時,h(0)=2﹣2ln1=2,
當n=e﹣1時,h(e﹣1)=e﹣1+2﹣2ln(e﹣1+1)=1+e﹣2=e﹣1<2,
則3﹣2ln2≤h(n)<2,
即n﹣m的取值范圍是[3﹣2ln2,2),
故選:A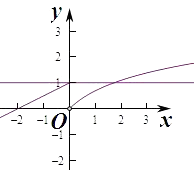


科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)求函數![]() 的單調區間;
的單調區間;
(2)試問:函數![]() 圖像上是否存在不同兩點
圖像上是否存在不同兩點![]() ,使得
,使得![]() 在
在![]() 處的切線
處的切線![]() 平行于直線
平行于直線![]() ,若存在,求出
,若存在,求出![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的極坐標方程是ρ=4cosθ.以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直l的參數方程是 ![]() (t是參數)
(t是參數)
(1)將曲線C的極坐標方程化為直角坐標方程;
(2)若直線l與曲線C相交于A、B兩點,且|AB|= ![]() ,求直線的傾斜角α的值.
,求直線的傾斜角α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某便利店計劃每天購進某品牌鮮奶若干件,便利店每銷售一瓶鮮奶可獲利![]() 元;若供大于求,剩余鮮奶全部退回,但每瓶鮮奶虧損
元;若供大于求,剩余鮮奶全部退回,但每瓶鮮奶虧損![]() 元;若供不應求,則便利店可從外調劑,此時每瓶調劑品可獲利
元;若供不應求,則便利店可從外調劑,此時每瓶調劑品可獲利![]() 元.
元.
(1)若便利店一天購進鮮奶![]() 瓶,求當天的利潤
瓶,求當天的利潤![]() (單位:元)關于當天鮮奶需求量
(單位:元)關于當天鮮奶需求量![]() (單位:瓶,
(單位:瓶,![]() )的函數解析式;
)的函數解析式;
(2)便利店記錄了![]() 天該鮮奶的日需求量
天該鮮奶的日需求量![]() (單位:瓶,
(單位:瓶,![]() )整理得下表:
)整理得下表:
日需求量 |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
若便利店一天購進![]() 瓶該鮮奶,以
瓶該鮮奶,以![]() 天記錄的各需求量的頻率作為各需求量發生的概率,求當天利潤在區間
天記錄的各需求量的頻率作為各需求量發生的概率,求當天利潤在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,某班一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,其中,頻率分布直方圖的分組區間分別為[50,60),[60,70),[70,80),[80,90),[90,100],據此解答如下問題. 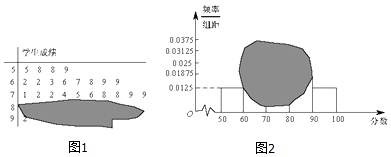
(Ⅰ)求全班人數及分數在[80,100]之間的頻率;
(Ⅱ)現從分數在[80,100]之間的試卷中任取 3 份分析學生情況,設抽取的試卷分數在[90,100]的份數為X,求X的分布列和數學望期.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是首項為正數的等比數列,公比為q,則“q<0”是“對任意的正整數n,a2n﹣1+a2n<0”的條件.(填“充要條件、充分不必要條件、必要不充分條件、即不充分也不必要條件”)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩地相距![]() ,貨車從甲地勻速行駛到乙地,速度不得超過
,貨車從甲地勻速行駛到乙地,速度不得超過![]() ,已知貨車每小時的運輸成本(單位:圓)由可變本和固定組成組成,可變成本是速度平方的
,已知貨車每小時的運輸成本(單位:圓)由可變本和固定組成組成,可變成本是速度平方的![]() 倍,固定成本為
倍,固定成本為![]() 元.
元.
(1)將全程勻速勻速成本![]() (元)表示為速度
(元)表示為速度![]() 的函數,并指出這個函數的定義域;
的函數,并指出這個函數的定義域;
(2)若![]() ,為了使全程運輸成本最小,貨車應以多大的速度行駛?
,為了使全程運輸成本最小,貨車應以多大的速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(sin(
=(sin( ![]() x+φ),1),
x+φ),1), ![]() =(1,cos(
=(1,cos( ![]() x+φ))(ω>0,0<φ<
x+φ))(ω>0,0<φ< ![]() ),記函數f(x)=(
),記函數f(x)=( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() ).若函數y=f(x)的周期為4,且經過點M(1,
).若函數y=f(x)的周期為4,且經過點M(1, ![]() ).
).
(1)求ω的值;
(2)當﹣1≤x≤1時,求函數f(x)的最值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com