
【題目】函數![]() ,
,![]() .
.
(1)若![]() ,設
,設![]() ,試證明
,試證明![]() 存在唯一零點
存在唯一零點![]() ,并求
,并求![]() 的最大值;
的最大值;
(2)若關于![]() 的不等式
的不等式![]() 的解集中有且只有兩個整數,求實數
的解集中有且只有兩個整數,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)根據零點存在性定理,首先證明函數的單調性,再證明存在區間![]() 使
使![]() 即證明;求函數的最大值,先求函數的導數求導函數的零點,并判斷零點兩側的單調性,即可求得函數的最大值;(2)不等式等價于
即證明;求函數的最大值,先求函數的導數求導函數的零點,并判斷零點兩側的單調性,即可求得函數的最大值;(2)不等式等價于![]() ,然后參變分離為
,然后參變分離為![]() ,利用導數分析函數
,利用導數分析函數![]() 以及函數
以及函數![]() ,根據所分析函數性質,當
,根據所分析函數性質,當![]() 時,只有2個正整數解,求
時,只有2個正整數解,求![]() 的取值范圍.
的取值范圍.
試題解析:(1)證明:由題意知![]() ,
,
于是![]()
令![]() ,
,![]() ,
,
∴![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
綜上![]() 存在唯一零點
存在唯一零點![]() .
.
解:當![]() ,于是
,于是![]() ,
,![]() 在
在![]() 單調遞增;
單調遞增;
當![]() ,于是
,于是![]() ,
,![]() 在
在![]() 單調遞減;
單調遞減;
故![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
故![]() .
.
(2)解:![]() 等價于
等價于![]() .
.
![]() ,
,
令![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,即
,即![]() 在
在![]() 上單調遞增.
上單調遞增.
又![]() ,
,
∴存在![]() ,使得
,使得![]() .
.
∴當![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 在
在![]() 上單調遞減.
上單調遞減.
∵![]() ,
,![]() ,
,
且當![]() 時,
時,![]() ,
,
又![]() ,
,![]() ,
,
故要使不等式![]() 解集中有且只有兩個整數,
解集中有且只有兩個整數,![]() 的取值范圍應為
的取值范圍應為![]()


科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,a、b、c分別為角A、B、C所對的邊,且 ![]() a=2csinA
a=2csinA
(1)確定角C的大小;
(2)若c= ![]() ,且△ABC的面積為
,且△ABC的面積為 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】請你設計一個包裝盒.如圖所示,ABCD是邊長為60 cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得A,B,C,D四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒.E、F在AB上,是被切去的一個等腰直角三角形斜邊的兩個端點.設AE=FB=x(cm).

(1)若廣告商要求包裝盒的側面積S(cm2)最大,試問x應取何值?
(2)某廠商要求包裝盒的容積V(cm3)最大,試問x應取何值?并求出此時包裝盒的高與底面邊長的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設矩形ABCD(AB>AD)的周長為24,把△ABC沿AC向△ADC折疊,AB折過去后交DC于點P,設AB=x,求△ADP的最大面積及相應x的值. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如圖,其中
所在平面互相垂直,如圖,其中![]() ,
,![]() ,
,![]() ,點
,點![]() 是線段
是線段![]() 的中點.
的中點.

(Ⅰ)試問在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 平面
平面![]() ?若存在,請證明
?若存在,請證明![]() 平面
平面![]() ,并求出
,并求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
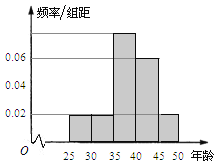
【題目】某單位![]() 名員工參加“我愛閱讀”活動,他們的年齡在25歲至50歲之間,按年齡分組:第1組
名員工參加“我愛閱讀”活動,他們的年齡在25歲至50歲之間,按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
(I)現要從年齡低于40歲的員工中用分層抽樣的方法抽取12人,則年齡在第![]() 組的員工人數分別是多少?
組的員工人數分別是多少?
(II)為了交流讀書心得,現從上述![]() 人中再隨機抽取
人中再隨機抽取![]() 人發言,設
人發言,設![]() 人中年齡在
人中年齡在![]() 的人數為
的人數為![]() ,求
,求![]() 的數學期望;
的數學期望;
(III)為了估計該單位員工的閱讀傾向,現對從該單位所有員工中按性別比例抽取的40人做“是否喜歡閱讀國學類書籍”進行調查,調查結果如下表所示:(單位:人)
喜歡閱讀國學類 | 不喜歡閱讀國學類 | 合計 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合計 | 22 | 18 | 40 |
根據表中數據,我們能否有![]() 的把握認為該單位員工是否喜歡閱讀國學類書籍和性別有關系?
的把握認為該單位員工是否喜歡閱讀國學類書籍和性別有關系?
附:![]() ,其中
,其中![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家具廠有方木料![]() ,五合板
,五合板![]() ,準備加工成書桌和書櫥出售.已知生產每張書桌需要方木料
,準備加工成書桌和書櫥出售.已知生產每張書桌需要方木料![]() ,五合板
,五合板![]() ,生產每個書櫥需要方木料
,生產每個書櫥需要方木料![]() ,五合板
,五合板![]() ,出售一張書桌可獲利潤
,出售一張書桌可獲利潤![]() 元,出售一個書櫥可獲利潤
元,出售一個書櫥可獲利潤![]() 元.
元.
(1)如果只安排生產書桌,可獲利潤多少?
(2)如果只安排生產書櫥,可獲利潤多少?
(3)怎樣安排生產可使所得利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖已知橢圓C: ![]() +y2=1,以橢圓的左頂點T為圓心作圓T:(x+2)2+y2=r2(r>0).設圓T與橢圓C交于點M與點N.
+y2=1,以橢圓的左頂點T為圓心作圓T:(x+2)2+y2=r2(r>0).設圓T與橢圓C交于點M與點N. 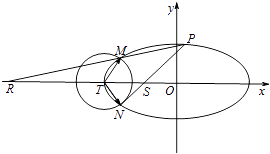
(1)求 ![]() 的最小值;
的最小值;
(2)設點P是橢圓C上異于M,N的任意一點,且直線MP,NP分別與x軸交于點R,S,O為坐標原點,求證:丨OR丨丨OS丨為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com