【題目】已知函數
．
（1）當
時，試求
在
處的切線方程；
（2）當
時，試求的單調區間；
（3）若在
內有極值，試求
的取值范圍．
【答案】（1）
；（2）單調增區間為
，單調減區間為
；（3）
．
【解析】
試題分析：（1）求導，利用導數的幾何意義求解；（2）求導，研究導函數的取值情況即可求解；（3）問題等價于
有解，求導后分析其取值情況即可．
試題解析：（1）當
時，
，
，
．方程為
；（2）0
，當
時，對于
，
恒成立，所以
，
；
，
，所以單調增區間為
，單調減區間為
；（3）若
在內有極值，則
在
內有解，令
，
，
，設
，
，所以
， 當時，
恒成立，所以
單調遞減，又因為
，又當
時，
，即
在上的值域為
，
所以當
時，
有解．
設
，則
，，所以
在單調遞減，
因為
，
，
所以
在有唯一解
，
所以有：
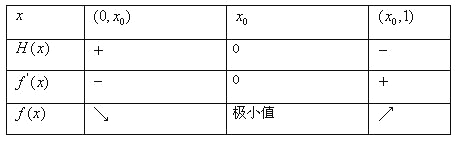
所以當
時，
在
內有極值且唯一，當
時，當時，
恒成立，
單調遞增，不成立，綜上，
的取值范圍為
．
小學學習好幫手系列答案
小學同步三練核心密卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f(x)=
g(x)=f(x)+
x-6lnx,其中
R.
(1)當=1時,判斷f(x)的單調性;
(2)當=2時,求出g(x)在（0,1）上的最大值；
(3)設函數
當=2時,若
總有
成立,求實數m的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在①
，
，②
，
，③
，
三個條件中任選一個補充在下面問題中，并加以解答.
已知
的內角A，B，C的對邊分別為a，b，c，若
，______，求的面積S.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一只小蜜蜂位于數軸上的原點處，小蜜蜂每一次具有只向左或只向右飛行一個單位或者兩個單位距離的能力，且每次飛行至少一個單位.若小蜜蜂經過5次飛行后，停在數軸上實數3位于的點處，則小蜜蜂不同的飛行方式有多少種？（ ）
A. 5 B. 25 C. 55 D. 75
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設某大學的女生體重y（單位：kg）與身高x（單位：cm）具有線性相關關系，根據一組樣本數據（xi，yi）（i=1，2，…，n），用最小二乘法建立的回歸方程為
=0.85x-85.71，則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心（
，
）
C. 若該大學某女生身高增加1cm，則其體重約增加0.85kg
D. 若該大學某女生身高為170cm，則可斷定其體重比為58.79kg
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
（
）的離心率
，直線
被以橢圓
的短軸為直徑的圓截得的弦長為
.
（1）求橢圓
的方程；
（2）過點
的直線
交橢圓于
， 
兩個不同的點，且
，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學為研究學生的身體素質與體育鍛煉時間的關系，對該校200名高三學生平均每天體育鍛煉時間進行調查，如表：（平均每天鍛煉的時間單位：分鐘）
平均每天鍛煉的時間/分鐘 |
|
|
|
|
|
|
總人數 | 20 | 36 | 44 | 50 | 40 | 10 |
將學生日均體育鍛煉時間在
的學生評價為“鍛煉達標”.
（1）請根據上述表格中的統計數據填寫下面的
列聯表；
鍛煉不達標 | 鍛煉達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
并通過計算判斷，是否能在犯錯誤的概率不超過0.025的前提下認為“鍛煉達標”與性別有關？
（2）在“鍛煉達標”的學生中，按男女用分層抽樣方法抽出5人，進行體育鍛煉體會交流，再從這5人中選出2人作重點發言，求作重點發言的2人中，至少1人是女生的概率.
參考公式：
，其中
.
臨界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
