
【題目】已知函數![]() (a為負整數)
(a為負整數)![]() 的圖像經過點
的圖像經過點![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)設函數![]() ,若
,若![]() 在
在![]() 上解集非空,求實數b的取值范圍;
上解集非空,求實數b的取值范圍;
(3)證明:方程![]() 有且僅有一個解.
有且僅有一個解.
【答案】(1)![]() .(2)
.(2)![]() (3)見解析﹔
(3)見解析﹔
【解析】
(1)在![]() 中令
中令![]() 得
得![]() ,故
,故![]() ,因為
,因為![]() 為負整數,所以
為負整數,所以![]() 為正整數,當
為正整數,當![]() 時,利用判別式可判斷此不等式無解,所以
時,利用判別式可判斷此不等式無解,所以![]() ,解得
,解得![]() ,從而可得
,從而可得![]() 的解析式;
的解析式;
(2)![]() 在
在![]() ,
,![]() 上解集非空轉化為
上解集非空轉化為![]() 在
在![]() ,
,![]() 上有解,再構造函數轉化為最小值可得;(3)即證
上有解,再構造函數轉化為最小值可得;(3)即證![]() 與
與![]() 的圖象有且只有一個交點,證明
的圖象有且只有一個交點,證明![]() 時,
時,![]() 與
與![]() 的圖象無交點,在
的圖象無交點,在![]() 上有且只有一個零點,即得證.
上有且只有一個零點,即得證.
(1)在![]() 中令
中令![]() 得
得![]() ,
,
![]() ,
,
因為![]() 為負整數,所以
為負整數,所以![]() 為正整數,
為正整數,
當![]() 時,
時,![]() ,因為△
,因為△![]() ,所以
,所以![]()
無解,
所以![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,
,
![]() ,
,
![]()
(2)![]() 在
在![]() ,
,![]() 上解集非空
上解集非空![]() 在
在![]() ,
,![]() 上有解,
上有解,
令![]() ,則
,則![]() ,
,
因為函數![]() 在
在![]() ,
,![]() 上是減函數,
上是減函數,
所以![]() 時,
時,![]() (3)
(3)![]() ,
,
故![]() .
.
(3)證明:即證![]() 與
與![]() 的圖象有且只有一個交點,
的圖象有且只有一個交點,
當![]() 時,
時,![]() ,
,
即![]() 時,
時,![]() 與
與![]() 的圖象無交點,
的圖象無交點,
當![]() 時,令
時,令![]() ,
,
因為函數![]() 在
在![]() 上為遞減函數,函數
上為遞減函數,函數![]() 在
在![]() 上為遞減函數,
上為遞減函數,
所以![]() 在
在![]() 上為遞減函數(減函數+減函數=減函數),
上為遞減函數(減函數+減函數=減函數),
又![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,根據零點存在性定理知:
,根據零點存在性定理知:![]() 在
在![]() 上有且只有一個零點,
上有且只有一個零點,
綜上得![]() 有且只有一個解.
有且只有一個解.


科目:高中數學 來源: 題型:
【題目】某市疾控中心流感監測結果顯示,自![]() 年
年![]() 月起,該市流感活動一度出現上升趨勢,尤其是
月起,該市流感活動一度出現上升趨勢,尤其是![]() 月以來,呈現快速增長態勢,截止目前流感病毒活動度仍處于較高水平,為了預防感冒快速擴散,某校醫務室采取積極方式,對感染者進行短暫隔離直到康復.假設某班級已知
月以來,呈現快速增長態勢,截止目前流感病毒活動度仍處于較高水平,為了預防感冒快速擴散,某校醫務室采取積極方式,對感染者進行短暫隔離直到康復.假設某班級已知![]() 位同學中有
位同學中有![]() 位同學被感染,需要通過化驗血液來確定感染的同學,血液化驗結果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗方法: 方案甲:逐個化驗,直到能確定感染同學為止;
位同學被感染,需要通過化驗血液來確定感染的同學,血液化驗結果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗方法: 方案甲:逐個化驗,直到能確定感染同學為止;
方案乙:先任取![]() 個同學,將它們的血液混在一起化驗,若結果呈陽性則表明感染同學為這
個同學,將它們的血液混在一起化驗,若結果呈陽性則表明感染同學為這![]() 位中的
位中的![]() 位,后再逐個化驗,直到能確定感染同學為止;若結果呈陰性則在另外
位,后再逐個化驗,直到能確定感染同學為止;若結果呈陰性則在另外![]() 位同學中逐個檢測;
位同學中逐個檢測;
(1)求依方案甲所需化驗次數等于方案乙所需化驗次數的概率;
(2)![]() 表示依方案甲所需化驗次數,
表示依方案甲所需化驗次數,![]() 表示依方案乙所需化驗次數,假設每次化驗的費用都相同,請從經濟角度考慮那種化驗方案最佳.
表示依方案乙所需化驗次數,假設每次化驗的費用都相同,請從經濟角度考慮那種化驗方案最佳.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax+bx﹣cx , 其中c>a>0,c>b>0.若a,b,c是△ABC的三條邊長,則下列結論中正確的是( )
①對一切x∈(﹣∞,1)都有f(x)>0;
②存在x∈R+ , 使ax , bx , cx不能構成一個三角形的三條邊長;
③若△ABC為鈍角三角形,則存在x∈(1,2),使f(x)=0.
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn,若Sm-1=-2,Sm=0,Sm+1=3,則m=( )
A. 5 B. 4 C. 3 D. 6
【答案】A
【解析】
根據數列前n項和的定義得到![]() 的值,再由數列的前n項和的公式得到
的值,再由數列的前n項和的公式得到![]() ,進而求得首項,由
,進而求得首項,由![]() =2,解得m值.
=2,解得m值.
Sm-1=-2,Sm=0,故得到![]() Sm=0,Sm+1=3,則
Sm=0,Sm+1=3,則![]() ,
,
根據等差數列的前n項和公式得到Sm=![]() ,得到首項為-2,故
,得到首項為-2,故![]() =2,解得m=5.
=2,解得m=5.
故答案為:A.
【點睛】
這個題目考查的是數列通項公式的求法及數列求和的常用方法;數列通項的求法中有常見的已知![]() 和
和![]() 的關系,求
的關系,求![]() 表達式,一般是寫出
表達式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
【題型】單選題
【結束】
11
【題目】已知等比數列{an}的各項均為不等于1的正數,數列{bn}滿足bn=lgan,b3=18,b6=12,則數列{bn}的前n項和的最大值等于( )
A. 126 B. 130 C. 132 D. 134
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于不等式![]() ,則對區間
,則對區間![]() 上的任意x都成立的實數t的取值范圍是_______.
上的任意x都成立的實數t的取值范圍是_______.
【答案】![]()
【解析】
根據二次函數的單調性求出x2﹣3x+2在區間[0,2]上的最小值和最大值,把問題轉化關于t的不等式組 得答案.
得答案.
∵x2﹣3x+2=![]() ,
,
∴當x∈[0,2]時,![]() ,(x2﹣3x+2)max=2.
,(x2﹣3x+2)max=2.
∴ .
.
∴對于不等式![]() (2t﹣t2)≤x2﹣3x+2≤3﹣t2,對區間[0,2]上任意x都成立的實數t的取值范圍是[﹣1,1﹣
(2t﹣t2)≤x2﹣3x+2≤3﹣t2,對區間[0,2]上任意x都成立的實數t的取值范圍是[﹣1,1﹣![]() ].
].
故答案為:[﹣1,1﹣![]() ].
].
【點睛】
本題考查函數恒成立問題,考查了不等式的解法,體現了數學轉化思想方法,是基礎題.二次不等式分含參二次不等式和不含參二次不等式;對于含參的二次不等式問題,先判斷二次項系數是否含參,接著討論參數等于0,不等于0,再看式子能否因式分解,若能夠因式分解則進行分解,再比較兩根大小,結合圖像得到不等式的解集.
【題型】填空題
【結束】
16
【題目】等差數列{an}的公差d≠0滿足![]() 成等比數列,若
成等比數列,若![]() =1,Sn是{
=1,Sn是{![]() }的前n項和,則
}的前n項和,則![]() 的最小值為________.
的最小值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是公比為正數的等比數列,
是公比為正數的等比數列,![]() ,
,![]()
(1)求![]() 的通項公式;
的通項公式;
(2)設![]() 是首項為1,公差為2的等差數列,求數列
是首項為1,公差為2的等差數列,求數列![]() 的前
的前![]() 項和
項和![]()
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)![]() 根據等比數列的通項公式得到:
根據等比數列的通項公式得到:![]() ,解得二次方程可得到
,解得二次方程可得到![]() 或
或![]() (舍去),進而得到數列的通項;(2)已知數列的類型是等差數列與等比數列求和的問題,根據等差等比數列求和公式得到結果即可.
(舍去),進而得到數列的通項;(2)已知數列的類型是等差數列與等比數列求和的問題,根據等差等比數列求和公式得到結果即可.
解:(1)設![]() 為等比數列
為等比數列![]() 的公比,則由
的公比,則由![]() ,
,![]() 得:
得:![]()
即![]() ,解得:
,解得:![]() 或
或![]() (舍去)
(舍去)
所以![]() 的通項公式為
的通項公式為![]()
(2) 由 等 差 數 列 的 通 項 公 式 得 到:![]()
由 等 差 數 列求 和 公 式 和 等 比 數 列 前 n 項 和 公 式 得 到
![]()
【點睛】
這個題目考查的是數列通項公式的求法及數列求和的常用方法;數列通項的求法中有常見的已知![]() 和
和![]() 的關系,求
的關系,求![]() 表達式,一般是寫出
表達式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等。
【題型】解答題
【結束】
18
【題目】設a≠b,解關于x的不等式a2x+b2(1-x)≥[ax+b(1-x)]2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從1至9這9個自然數中任取兩個:
![]() 恰有一個偶數和恰有一個奇數;
恰有一個偶數和恰有一個奇數;![]() 至少有一個是奇數和兩個數都是奇數;
至少有一個是奇數和兩個數都是奇數;
![]() 至多有一個奇數和兩個數都是奇數;
至多有一個奇數和兩個數都是奇數;![]() 至少有一個奇數和至少有一個偶數.
至少有一個奇數和至少有一個偶數.
在上述事件中,是對立事件的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在直角坐標系![]() 中, 直線
中, 直線![]() 的參數方程為是
的參數方程為是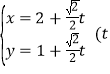 為參數), 以坐標原點
為參數), 以坐標原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系, 曲線
軸正半軸為極軸建立極坐標系, 曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1) 判斷直線![]() 與曲線
與曲線![]() 的位置關系;
的位置關系;
(2) 在曲線![]() 上求一點
上求一點![]() ,使得它到直線
,使得它到直線![]() 的距離最大,并求出最大距離.
的距離最大,并求出最大距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com