
【題目】已知有窮數列A:![]() (
(![]() 且
且![]() ).定義數列A的“伴生數列”B:
).定義數列A的“伴生數列”B:![]() ,其中
,其中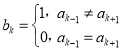 (
(![]() ),規定
),規定![]() ,
,![]() .
.
(1)寫出下列數列的“伴生數列”:
①1,2,3,4,5;
②1,![]() ,1,
,1,![]() ,1.
,1.
(2)已知數列B的“伴生數列”C:![]() ,
,![]() ,…,
,…,![]() ,…,
,…,![]() ,且滿足
,且滿足![]() (
(![]() ,2,…,n).
,2,…,n).
(i)若數列B中存在相鄰兩項為1,求證:數列B中的每一項均為1;
(ⅱ)求數列C所有項的和.
【答案】(1)①1,1,1,1,1②1,0,0,0,1(2)(i)證明見解析(ⅱ)所有項的和![]() 或
或![]() (n是3的倍數)
(n是3的倍數)
【解析】
(1)根據“伴生數列”的定義求解即可;
(2)(i)設存在![]() ,使得
,使得![]() ,討論
,討論![]() 和
和![]() ,結合“伴生數列”的定義證明即可;
,結合“伴生數列”的定義證明即可;
(ⅱ)利用反證法得出不可能存在![]() ,
,![]() ,再對數列
,再對數列![]() 的前三項
的前三項![]() ,
,![]() ,
,![]() 的值進行討論,當
的值進行討論,當![]() 時,得出所有項的和
時,得出所有項的和![]() ;當
;當![]() ,
,![]() ,
,![]() 時,得出
時,得出![]() 與已知矛盾;當
與已知矛盾;當![]() ,
,![]() ,
,![]() 時,結合“伴生數列”的定義得出所有項的和
時,結合“伴生數列”的定義得出所有項的和![]() ,同理可以得出當
,同理可以得出當![]() ,
,![]() ,
,![]() 及
及![]() ,
,![]() ,
,![]() 時,所有項的和
時,所有項的和![]() .
.
解:(1)①1,1,1,1,1;
②1,0,0,0,1.
(2)(i)由題意,存在![]() ,使得
,使得![]() .
.
若![]() ,即
,即![]() 時,
時,![]() .
.
于是![]() ,
,![]() .
.
所以![]() ,所以
,所以![]() .即
.即![]() .
.
依次類推可得![]() (
(![]() ,3,…,
,3,…,![]() ).
).
所以![]() (
(![]() ,2,…,n).
,2,…,n).
若![]() ,由
,由![]() 得
得![]() .
.
于是![]() .所以
.所以![]() .
.
依次類推可得![]() .
.
所以![]() (
(![]() ,2,…,n).
,2,…,n).
綜上可知,數列B中的每一項均為1.
(ⅱ)首先證明不可能存在![]() 使得
使得![]() .
.
若存在![]() 使得
使得![]() ,
,
則![]() .
.
又![]() 得
得![]() 與已知矛盾.
與已知矛盾.
所以不可能存在![]() ,
,![]() .
.
由此及(ⅰ)得數列![]() 的前三項
的前三項![]() ,
,![]() ,
,![]() 的可能情況如下:
的可能情況如下:
當![]() 時,由(i)可得
時,由(i)可得![]() (
(![]() ,2,…,n).
,2,…,n).
于是![]() (
(![]() ,2,…,n)
,2,…,n)![]() .
.
所以所有項的和![]() .
.
當![]() ,
,![]() ,
,![]() 時,
時,![]() ,
,
此時![]() 與已知矛盾.
與已知矛盾.
當![]() ,
,![]() ,
,![]() 時,
時,![]() ,
,![]() ,
,![]() .
.
于是![]() ,
,![]() .
.
故![]() ,
,![]() ,
,![]()
于是![]() ,
,![]() ,
,![]() ,
,
于是![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
依次類推![]() 且n恰是3的倍數滿足題意.
且n恰是3的倍數滿足題意.
所以所有項的和![]() .
.
同理可得![]() ,
,![]() ,
,![]() 及
及![]() ,
,![]() ,
,![]() 時,
時,
當且僅當n恰是3的倍數時,滿足題意.
此時所有項的和![]() .
.
綜上,所有項的和![]() 或
或![]() (n是3的倍數).
(n是3的倍數).


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S﹣ABCD中,側面SCD為鈍角三角形且垂直于底面ABCD,CD=SD,點M是SA的中點,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.
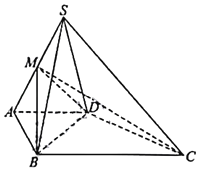
(1)求證:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱錐C﹣MBD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為![]() (t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為
(t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求曲線C的直角坐標方程及直線l的普通方程;
(2)將所得曲線C向右平移1個單位長度,再將曲線C上的所有點的橫坐標變為原來的2倍,得到曲線![]() ,求曲線
,求曲線![]() 上的點到直線l的距離的最大值.
上的點到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果對某對象連續實施兩次變換后的結果就是變換前的對象,那么我們稱這種變換為“回歸”變換.如:對任意一個實數,變換:取其相反數.因為相反數的相反數是它本身,所以變換“取實數的相反數”是一種“回歸”變換.有下列3種變換:
①對![]() ,變換:求集合A的補集;
,變換:求集合A的補集;
②對任意![]() ,變換:求z的共軛復數;
,變換:求z的共軛復數;
③對任意![]() ,變換:
,變換:![]() (k,b均為非零實數).
(k,b均為非零實數).
其中是“回歸”變換的是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
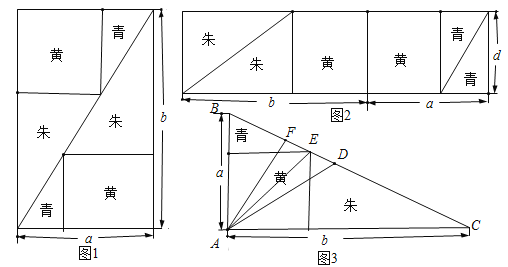
【題目】《九章算術》中“勾股容方”問題:“今有勾五步,股十二步,問勾中容方幾何?”魏晉時期數學家劉徽在其《九章算術注》中利用出入相補原理給出了這個問題的一般解法:如圖1,用對角線將長和寬分別為![]() 和
和![]() 的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為
的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為![]() ,寬為內接正方形的邊長
,寬為內接正方形的邊長![]() .由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設
.由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設![]() 為斜邊
為斜邊![]() 的中點,作直角三角形
的中點,作直角三角形![]() 的內接正方形對角線
的內接正方形對角線![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,則下列推理正確的是( )
,則下列推理正確的是( )
①由圖1和圖2面積相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得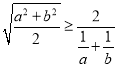 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:min)繪制了莖葉圖:則下列結論中表述不正確的是
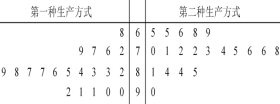
A. 第一種生產方式的工人中,有75%的工人完成生產任務所需要的時間至少80分鐘
B. 第二種生產方式比第一種生產方式的效率更高
C. 這40名工人完成任務所需時間的中位數為80
D. 無論哪種生產方式的工人完成生產任務平均所需要的時間都是80分鐘.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的普通方程為:
的普通方程為:![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,正方形
,正方形![]() 的頂點都在
的頂點都在![]() 上,且
上,且![]() 逆時針依次排列,點
逆時針依次排列,點![]() 的極坐標為
的極坐標為![]()
(1)寫出曲線![]() 的參數方程,及點
的參數方程,及點![]() 的直角坐標;
的直角坐標;
(2)設![]() 為橢圓
為橢圓![]() 上的任意一點,求:
上的任意一點,求:![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了實施“科技下鄉,精準脫貧”戰略,某縣科技特派員帶著![]() 三個農業扶貧項目進駐某村,對僅有的四個貧困戶進行產業幫扶.經過前期走訪得知,這四個貧困戶甲、乙、丙、丁選擇
三個農業扶貧項目進駐某村,對僅有的四個貧困戶進行產業幫扶.經過前期走訪得知,這四個貧困戶甲、乙、丙、丁選擇![]() 三個項目的意向如下:
三個項目的意向如下:
扶貧項目 |
|
|
|
貧困戶 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每個貧困戶只能從自己已登記的選擇意向中隨機選取一項,且每個項目至多有兩個貧困戶選擇,則甲乙兩戶選擇同一個扶貧項目的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com