
(本題16分)函數(shù)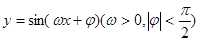 在同一個周期內(nèi),當
在同一個周期內(nèi),當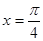 時
時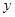 取最大值1,當
取最大值1,當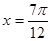 時,
時,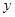 取最小值
取最小值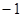 。
。
(1)求函數(shù)的解析式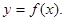
(2)函數(shù)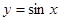 的圖象經(jīng)過怎樣的變換可得到
的圖象經(jīng)過怎樣的變換可得到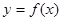 的圖象?
的圖象?
(3)若函數(shù)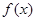 滿足方程
滿足方程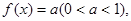 求在
求在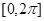 內(nèi)的所有實數(shù)根之和.
內(nèi)的所有實數(shù)根之和.
(1) 函數(shù)
函數(shù)
(2)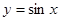 的圖象向右平移
的圖象向右平移 個單位得
個單位得 的圖象
的圖象
再由 圖象上所有點的橫坐標變?yōu)樵瓉淼?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052023251557811554/SYS201205202326545625828022_DA.files/image007.png">.縱坐標不變,得到
圖象上所有點的橫坐標變?yōu)樵瓉淼?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052023251557811554/SYS201205202326545625828022_DA.files/image007.png">.縱坐標不變,得到 的圖象,
的圖象,
(3)所有實數(shù)之和為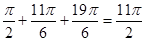
【解析】解:(1)
又因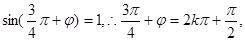
又
 函數(shù)
函數(shù)
(2)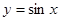 的圖象向右平移
的圖象向右平移 個單位得
個單位得 的圖象
的圖象
再由 圖象上所有點的橫坐標變?yōu)樵瓉淼?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052023251557811554/SYS201205202326545625828022_DA.files/image007.png">.縱坐標不變,得到
圖象上所有點的橫坐標變?yōu)樵瓉淼?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052023251557811554/SYS201205202326545625828022_DA.files/image007.png">.縱坐標不變,得到 的圖象,
的圖象,
(3)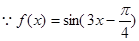 的周期為
的周期為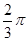
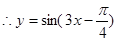 在
在 內(nèi)恰有3個周期,
內(nèi)恰有3個周期,
并且方程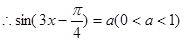 在
在 內(nèi)有6個實根且
內(nèi)有6個實根且
同理,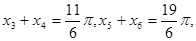
故所有實數(shù)之和為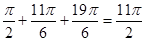


 勵耘書業(yè)暑假銜接寧波出版社系列答案
勵耘書業(yè)暑假銜接寧波出版社系列答案科目:高中數(shù)學 來源:2012屆江蘇省泰州中學高三上學期期中考試數(shù)學 題型:解答題
(本題滿分16分)設函數(shù)y=f(x)對任意實數(shù)x,都有f(x)=2f(x+1),當x∈[0,1]時,f(x)=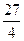 x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,當x∈[n,n+1]時,求y=f(x)的解析式;
(Ⅱ)求證:對于任意的n∈N+,當x∈[n,n+1]時,都有|f(x)|≤ ;
;
(Ⅲ)對于函數(shù)y=f(x) (x∈[0,+∞
(x∈[0,+∞ ,若在它的圖象上存在點P,使經(jīng)過點P的切線與直線x+y=1平行,那么這樣點有多少個?并說明理由
,若在它的圖象上存在點P,使經(jīng)過點P的切線與直線x+y=1平行,那么這樣點有多少個?并說明理由
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年上海市高三上學期期中考試理科數(shù)學試卷 題型:解答題
(本題16分)已知函數(shù) 在定義域
在定義域 上是奇函數(shù),(其中
上是奇函數(shù),(其中 且
且 ).
).
(1)求出 的值,并求出定義域
的值,并求出定義域 ;
;
(2)判斷 在
在 上的單調(diào)性,并用定義加以證明;
上的單調(diào)性,并用定義加以證明;
(3)當 時,
時, 的值域范圍恰為
的值域范圍恰為 ,求
,求 及
及 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源:江蘇省09-10學年度第一學期第三次月考高一數(shù)學 題型:解答題
(本題16分)函數(shù)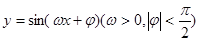 在同一個周期內(nèi),當
在同一個周期內(nèi),當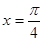 時
時 取最大值1,當
取最大值1,當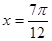 時,
時, 取最小值
取最小值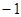 。
。
(1)求函數(shù)的解析式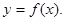
(2)函數(shù)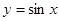 的圖象經(jīng)過怎樣的變換可得到
的圖象經(jīng)過怎樣的變換可得到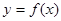 的圖象?
的圖象?
(3)若函數(shù)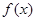 滿足方程
滿足方程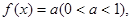 求在
求在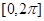 內(nèi)的所有實數(shù)根之和.
內(nèi)的所有實數(shù)根之和.
查看答案和解析>>
科目:高中數(shù)學 來源:2010年江蘇省南通市高一上學期期中考試數(shù)學試卷 題型:解答題
(本題滿分16分)設函數(shù)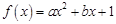
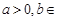 R
的最小值為-a,
R
的最小值為-a,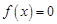 兩個實根為
兩個實根為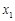 、
、 .[來源:Z。xx。k.Com]
.[來源:Z。xx。k.Com]
(1)求 的值;
的值;
(2)若關于 的不等式
的不等式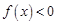 解集為
解集為 ,函數(shù)
,函數(shù)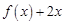 在
在 上不存在最小值,求
上不存在最小值,求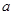 的取值范圍;
的取值范圍;
(3)若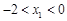 ,求b的取值范圍。
,求b的取值范圍。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com