
【題目】設(shè)數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() (
(![]() ),設(shè)
),設(shè)![]() (
(![]() ),數(shù)列
),數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)利用“歸納—猜想—證明”求出![]() 的通項公式;
的通項公式;
(3)求數(shù)列![]() 的通項公式.
的通項公式.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() (
(![]() );(3)
);(3)![]() .
.
【解析】
(1)先代![]() ,求得
,求得![]() ,當(dāng)
,當(dāng)![]() 時,根據(jù)
時,根據(jù)![]() ,化簡得到
,化簡得到![]() 與
與![]() 的遞推式,
的遞推式,
再代![]() ,求得
,求得![]() ,并為求第(2)問提供基礎(chǔ);
,并為求第(2)問提供基礎(chǔ);
(2)由(1)歸納猜想![]() ,并用數(shù)學(xué)歸納法證明;
,并用數(shù)學(xué)歸納法證明;
(3)由(2)求得的![]() ,求出
,求出![]() ,并化簡
,并化簡![]() ,分析
,分析![]() ,發(fā)現(xiàn)可用裂項相消法求解,
,發(fā)現(xiàn)可用裂項相消法求解,
考慮消去方便,可對![]() 分奇數(shù)和偶數(shù)兩種情況分析,最后合并得到答案.
分奇數(shù)和偶數(shù)兩種情況分析,最后合并得到答案.
解:(1)由![]() ,令
,令![]() ,則
,則![]() ,得
,得![]() ,
,
當(dāng)![]() 時,由
時,由![]() ,得
,得![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() ,猜想
,猜想![]() ,
,
下面用數(shù)學(xué)歸納法證明:① 當(dāng)![]() 時,由猜想知顯然成立;
時,由猜想知顯然成立;
②假設(shè)![]() 猜想成立,即
猜想成立,即![]() ,
,
則當(dāng)![]() 時,由(1)有
時,由(1)有![]()
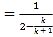
![]() ,
,
即當(dāng)![]() 時,猜想
時,猜想![]() 也成立.
也成立.
綜合①②可知,猜想![]() 成立,即
成立,即![]()
(3)由(2)知![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]()
![]()
![]() ,
,
綜合知:![]() ,又
,又![]() ,
,
則![]()
![]()
![]()
當(dāng)![]() 為偶數(shù)時,
為偶數(shù)時,
![]()
![]()
![]()
![]()
![]()
當(dāng)![]() 為奇數(shù)時,
為奇數(shù)時,![]()
![]()
![]()
![]()
![]()
![]()
![]()
綜上可得![]()


 同步練習(xí)河南大學(xué)出版社系列答案
同步練習(xí)河南大學(xué)出版社系列答案 同步練習(xí)西南大學(xué)出版社系列答案
同步練習(xí)西南大學(xué)出版社系列答案 補(bǔ)充習(xí)題江蘇系列答案
補(bǔ)充習(xí)題江蘇系列答案 學(xué)練快車道口算心算速算天天練系列答案
學(xué)練快車道口算心算速算天天練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校從參加環(huán)保知識競賽的1200名學(xué)生中,隨機(jī)抽取60名,將其成績(均為整數(shù))分成六段![]() ,
,![]() ,…,
,…,![]() 后畫出如圖的頻率分布直方圖.
后畫出如圖的頻率分布直方圖.
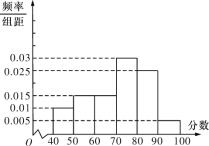
(1)估計這次競賽成績的眾數(shù)與中位數(shù)(結(jié)果保留小數(shù)點(diǎn)后一位);
(2)若這次競賽成績不低于80分的同學(xué)都可以獲得一份禮物,試估計該校參加競賽的1200名學(xué)生中可以獲得禮物的人數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某單位的食堂中,食堂每天以![]() 元/斤的價格購進(jìn)米粉,然后以4.4元/碗的價格出售,每碗內(nèi)含米粉0.2斤,如果當(dāng)天賣不完,剩下的米粉以2元/斤的價格賣給養(yǎng)豬場.根據(jù)以往統(tǒng)計資料,得到食堂某天米粉需求量的頻率分布直方圖如圖所示,若食堂某天購進(jìn)了80斤米粉,以
元/斤的價格購進(jìn)米粉,然后以4.4元/碗的價格出售,每碗內(nèi)含米粉0.2斤,如果當(dāng)天賣不完,剩下的米粉以2元/斤的價格賣給養(yǎng)豬場.根據(jù)以往統(tǒng)計資料,得到食堂某天米粉需求量的頻率分布直方圖如圖所示,若食堂某天購進(jìn)了80斤米粉,以![]() (單位:斤)(其中
(單位:斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (單位:元)表示利潤.
(單位:元)表示利潤.
(Ⅰ)計算當(dāng)天米粉需求量的平均數(shù),并直接寫出需求量的眾數(shù)和中位數(shù);
(Ⅱ) 將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(Ⅲ)根據(jù)直方圖估計該天食堂利潤不少于760元的概率.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某班同學(xué)利用國慶節(jié)進(jìn)行社會實(shí)踐,對[25,55]歲的人群隨機(jī)抽取![]() 人進(jìn)行了一次生活習(xí)慣是否符合低碳觀念的調(diào)查,若生活習(xí)慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統(tǒng)計表和各年齡段人數(shù)頻率分布直方圖:
人進(jìn)行了一次生活習(xí)慣是否符合低碳觀念的調(diào)查,若生活習(xí)慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統(tǒng)計表和各年齡段人數(shù)頻率分布直方圖:
組數(shù) | 分組 | 低碳族的人數(shù) | 占本組的頻率 |
第一組 | [25,30) | 120 | 0.6 |
第二組 | [30,35) | 195 |
|
第三組 | [35,40) | 100 | 0.5 |
第四組 | [40,45) |
| 0.4 |
第五組 | [45,50) | 30 | 0.3 |
第六組 | [50,55] | 15 | 0.3 |
(1)補(bǔ)全頻率分布直方圖并求![]() 的值;
的值;
(2)從年齡段在[40,50)的“低碳族”中采用分層抽樣法抽取6人參加戶外低碳體驗(yàn)活動,其中選取2人作為領(lǐng)隊,求選取的2名領(lǐng)隊中恰有1人年齡在[4,45)歲的概率.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列{an}滿足當(dāng)n>1時,an=![]() ,且a1=
,且a1=![]() .
.
(1)求證:數(shù)列![]() 為等差數(shù)列;
為等差數(shù)列;
(2)a1a2是否是數(shù)列{an}中的項?如果是,求出是第幾項;如果不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]() .
.
(1)求f(2)+f(![]() ),f(3)+f(
),f(3)+f(![]() )的值;
)的值;
(2)求證:f(x)+f(![]() )是定值;
)是定值;
(3)求f(2)+f(![]() )+f(3)+f(
)+f(3)+f(![]() )+…+f(2012)+f(
)+…+f(2012)+f(![]() )的值.
)的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】高考復(fù)習(xí)經(jīng)過二輪“見多識廣”之后,為了研究考前“限時搶分”強(qiáng)化訓(xùn)練次數(shù)![]() 與答題正確率
與答題正確率![]() ﹪的關(guān)系,對某校高三某班學(xué)生進(jìn)行了關(guān)注統(tǒng)計,得到如下數(shù)據(jù):
﹪的關(guān)系,對某校高三某班學(xué)生進(jìn)行了關(guān)注統(tǒng)計,得到如下數(shù)據(jù):
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,并預(yù)測答題正確率是100﹪的強(qiáng)化訓(xùn)練次數(shù);
的線性回歸方程,并預(yù)測答題正確率是100﹪的強(qiáng)化訓(xùn)練次數(shù);
(2)若用![]() 表示統(tǒng)計數(shù)據(jù)的“強(qiáng)化均值”(精確到整數(shù)),若“強(qiáng)化均值”的標(biāo)準(zhǔn)差在區(qū)間
表示統(tǒng)計數(shù)據(jù)的“強(qiáng)化均值”(精確到整數(shù)),若“強(qiáng)化均值”的標(biāo)準(zhǔn)差在區(qū)間![]() 內(nèi),則強(qiáng)化訓(xùn)練有效,請問這個班的強(qiáng)化訓(xùn)練是否有效?
內(nèi),則強(qiáng)化訓(xùn)練有效,請問這個班的強(qiáng)化訓(xùn)練是否有效?
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
![]() =
= ,
, ![]() =
=![]() -
-![]()
![]() ,
,
樣本數(shù)據(jù)![]() 的標(biāo)準(zhǔn)差為:
的標(biāo)準(zhǔn)差為: 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 有兩個不相等的正零點(diǎn),求
有兩個不相等的正零點(diǎn),求![]() 的取值范圍;
的取值范圍;
(2)若函數(shù)![]() 在
在![]() 上的最小值為-3,求
上的最小值為-3,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com