【題目】如圖，在三棱柱
中，點
是
的中點，欲過點
作一截面與平面
平行．
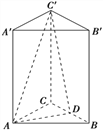
(I)問應當怎樣畫線，并說明理由；
(II)求所作截面與平面
將三棱柱分成的三部分的體積之比．
【答案】(I)見解析 (II)1:4:1
【解析】試題(I) 在三棱柱
中，點
是
的中點，取
的中點
，連接
， 
， 
，則平面
∥平面
， 
即為應畫的線．可以證得平面
(II) 
三棱柱夾在平面
與平面
間的體積為
即得體積比.
試題解析：
(I)在三棱柱
中，點
是
的中點，取
的中點
，連接
， 
， 
，則平面
∥平面
， 
即為應畫的線．理由如下：因為
為
的中點， 
為
的中點，所以
.又因為
∥
，所以四邊形
為平行四邊形，所以
∥
. 
. 
.
.連接
，則
平行等于
，所以
平行等于
，所以四邊形
是平行四邊形，所以
∥
. 
. 
.
.又因為
， 
， 
,
所以平面
.
(II)設棱柱的底面積為
，高為
.
則
所以三棱柱夾在平面
與平面
間的體積為
∴所作截面與平面
將三棱柱分成的三部分的體積之比為
.
輕松奪冠全能掌控卷系列答案科目：高中數學 來源： 題型：
【題目】為了解某城市居民的月平均用電量情況，隨機抽查了該城市100戶居民的月平均用電量（單位：度），得到頻率分布直方圖（如圖所示）.數據的分組依次為
、
、
、
、
、
、
.
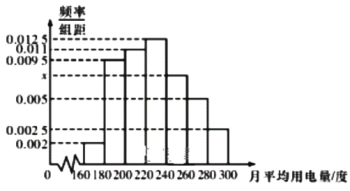
（1）求頻率分布直方圖中
的值；
（2）求該城市所有居民月平均用電量的眾數和中位數的估計值；
（3）在月平均用電量為
的四組用戶中，采用分層抽樣的方法抽取
戶居民，則應從月用電量在居民中抽取多少戶？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】汽車是碳排放量比較大的交通工具,某地規定,從2017年開始,將對二氧化碳排放量超過130 g/km的輕型汽車進行懲罰性征稅,檢測單位對甲、乙兩品牌輕型汽車各抽取5輛進行二氧化碳排放量檢測,記錄如下(單位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | 100 | 160 |
經測算得乙品牌輕型汽車二氧化碳排放量的平均值為
=120 g/km.
(1)求表中x的值,并比較甲、乙兩品牌輕型汽車二氧化碳排放量的穩定性;
(2)從被檢測的5輛甲品牌輕型汽車中任取2輛,則至少有一輛二氧化碳排放量超過130 g/km的概率是多少?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2018屆安徽省合肥市高三第一次教學質量檢測】一家大型購物商場委托某機構調查該商場的顧客使用移動支付的情況.調查人員從年齡在
內的顧客中，隨機抽取了180人，調查結果如表：
（1）為推廣移動支付，商場準備對使用移動支付的顧客贈送1個環保購物袋.若某日該商場預計有12000人購物，試根據上述數據估計，該商場當天應準備多少個環保購物袋？
（2）某機構從被調查的使用移動支付的顧客中，按分層抽樣的方式抽取7人作跟蹤調查，并給其中2人贈送額外禮品，求獲得額外禮品的2人年齡都在
內的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某醫藥研究所開發的一種新藥，如果成年人按規定的劑量服用，據監測：服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線．
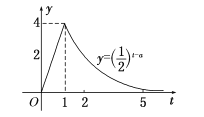
(1)寫出第一次服藥后，y與t之間的函數關系式y＝f(t)；
(2)據進一步測定：每毫升血液中含藥量不少于0.25微克時，治療有效．求服藥一次后治療有效的時間是多長？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標平面內，以坐標原點
為極點， 
軸的非負半軸為極軸建立極坐標系.已知點
、
的極坐標分別為
、
，曲線
的參數方程為
（
為參數）.
（1）求直線
的直角坐標方程；
（2）若直線
和曲線
只有一個交點，求
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
