
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,記函數
時,記函數![]() 在
在![]() 上的最大值為
上的最大值為![]() ,最小值為
,最小值為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】“互聯網![]() ”是“智慧城市”的重要內士,
”是“智慧城市”的重要內士,![]() 市在智慧城市的建設中,為方便市民使用互聯網,在主城區覆蓋了免費
市在智慧城市的建設中,為方便市民使用互聯網,在主城區覆蓋了免費![]() .為了解免費
.為了解免費![]() 在
在![]() 市的使用情況,調査機構借助網絡進行了問卷調查,并從參與調査的網友中抽取了
市的使用情況,調査機構借助網絡進行了問卷調查,并從參與調査的網友中抽取了![]() 人進行抽樣分析,得到如下列聯表(單位:人):
人進行抽樣分析,得到如下列聯表(單位:人):
經常使用免費WiFi | 偶爾或不用免費WiFi | 合計 | |
45歲及以下 | 70 | 30 | 100 |
45歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據以上數據,判斷是否有![]() 的把握認為
的把握認為![]() 市使用免費
市使用免費![]() 的情況與年齡有關;
的情況與年齡有關;
(2)將頻率視為概率,現從該市![]() 歲以上的市民中用隨機抽樣的方法每次抽取
歲以上的市民中用隨機抽樣的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.記被抽取的
次.記被抽取的![]() 人中“偶爾或不用免費
人中“偶爾或不用免費![]() ”的人數為
”的人數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列,數學期望
的分布列,數學期望![]() 和方差
和方差![]() .
.
附: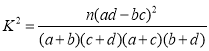 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線![]() 經過點
經過點![]() ,傾斜角
,傾斜角![]() ,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線
,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線![]() .
.
(Ⅰ)求曲線C的直角坐標方程并寫出直線l的參數方程;
(Ⅱ)直線l與曲線C的交點為A,B,求點P到A、B兩點的距離之積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“珠算之父”程大位是我國明代著名的數學家,他的應用巨著《算法統綜》中有一首“竹筒容米”問題:“家有九節竹一莖,為因盛米不均平,下頭三節四升五,上梢四節三升八,唯有中間兩節竹,要將米數次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容積依次相差同一數量.)用你所學的數學知識求得中間兩節竹的容積為
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為4的正方形,
是邊長為4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是線段
是線段![]() 上一點,求三棱錐
上一點,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)利用“五點法”畫出函數![]() 在長度為一個周期的閉區間的簡圖.
在長度為一個周期的閉區間的簡圖.
列表:
| |||||
x | |||||
y |
作圖:
(2)并說明該函數圖象可由![]() 的圖象經過怎么變換得到的.
的圖象經過怎么變換得到的.
(3)求函數![]() 圖象的對稱軸方程.
圖象的對稱軸方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com