
【題目】f(x)是定義在D上的函數,若存在區間[m,n]D,使函數f(x)在[m,n]上的值域恰為[km,kn],則稱函數f(x)是k型函數.給出下列說法:①f(x)=3﹣ ![]() 不可能是k型函數; ②若函數y=﹣
不可能是k型函數; ②若函數y=﹣ ![]() x2+x是3型函數,則m=﹣4,n=0;
x2+x是3型函數,則m=﹣4,n=0;
③設函數f(x)=x3+2x2+x(x≤0)是k型函數,則k的最小值為 ![]() ;
;
④若函數y= ![]() (a≠0)是1型函數,則n﹣m的最大值為
(a≠0)是1型函數,則n﹣m的最大值為 ![]() .
.
下列選項正確的是( )
A.①③
B.②③
C.②④
D.①④
【答案】C
【解析】解:對于①,f(x)的定義域是{x|x≠0},且f(2)=3﹣ ![]() =1,f(4)=3﹣
=1,f(4)=3﹣ ![]() =2, ∴f(x)在[2,4]上的值域是[1,2],f(x)是
=2, ∴f(x)在[2,4]上的值域是[1,2],f(x)是 ![]() 型函數,
型函數,
∴①錯誤;
對于②,y=﹣ ![]() x2+x是3型函數,即﹣
x2+x是3型函數,即﹣ ![]() x2+x=3x,解得x=0,或x=﹣4,∴m=﹣4,n=0,
x2+x=3x,解得x=0,或x=﹣4,∴m=﹣4,n=0,
∴②正確;
對于③,f(x)=x3+2x2+x(x≤0)是k型函數,則x3+2x2+x=kx有二不等負實數根,
即x2+2x+(1﹣k)=0有二不等負實數根,
∴ ![]() ,解得0<k<1,
,解得0<k<1,
∴③錯誤;
對于④,y= ![]() (a≠0)是1型函數,即(a2+a)x﹣1=a2x2 , ∴a2x2﹣(a2+a)x+1=0,
(a≠0)是1型函數,即(a2+a)x﹣1=a2x2 , ∴a2x2﹣(a2+a)x+1=0,
∴方程的兩根之差x1﹣x2= ![]() =
= ![]() =
= ![]()
= ![]() ≤
≤ ![]() ,即n﹣m的最大值為
,即n﹣m的最大值為 ![]() ,∴④正確.
,∴④正確.
綜上,正確的命題是②④.
故選:C.
根據題目中的新定義,結合函數與方程的知識,逐一判定命題①②③④是否正確,從而確定正確的答案.


 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,Sn=2n﹣an(n∈N*).
(1)計算a2 , a3 , a4 , 并由此猜想通項公式an;
(2)用數學歸納法證明(1)中的猜想.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax2+(b﹣1)x+3.
(1)若不等式f(x)>0的解為(﹣1, ![]() ),求不等式bx2﹣3x+a≤0的解集;
),求不等式bx2﹣3x+a≤0的解集;
(2)若f(1)=4,a>0,b>0,求ab的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個不透明的袋子裝有4個完全相同的小球,球上分別標有數字為0,1,2,2,現甲從中摸出一個球后便放回,乙再從中摸出一個球,若摸出的球上數字大即獲勝(若數字相同則為平局),則在甲獲勝的條件下,乙摸1號球的概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】請你設計一個包裝盒,如圖所示,ABCD是邊長為60cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得A,B,C,D四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,E、F在AB上,是被切去的等腰直角三角形斜邊的兩個端點,設AE=FB=x(cm). 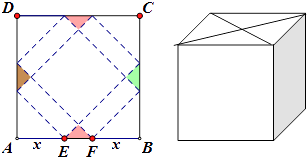
(1)若廣告商要求包裝盒側面積S(cm2)最大,試問x應取何值?
(2)若廣告商要求包裝盒容積V(cm3)最大,試問x應取何值?并求出此時包裝盒的高與底面邊長的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1+lnx﹣ ![]() ,其中k為常數.
,其中k為常數.
(1)若k=0,求曲線y=f(x)在點(1,f(1))處的切線方程.
(2)若k=5,求證:f(x)有且僅有兩個零點;
(3)若k為整數,且當x>2時,f(x)>0恒成立,求k的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,A、B、C是三角形的三內角,a、b、c是三內角對應的三邊,已知b2 , a2 , c2成等差數列.
(1)求cosA的最小值;
(2)若a=2,當A最大時,△ABC面積的最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=a﹣x2( ![]() ≤x≤e,e為自然對數的底數)與h(x)=2lnx的圖象上存在關于x軸對稱的點,則實數a的取值范圍是( )
≤x≤e,e為自然對數的底數)與h(x)=2lnx的圖象上存在關于x軸對稱的點,則實數a的取值范圍是( )
A.[1, ![]() +2]
+2]
B.[1,e2﹣2]
C.[ ![]() +2,e2﹣2]
+2,e2﹣2]
D.[e2﹣2,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com