
【題目】函數f(x)=loga(ax+1)+mx是偶函數.
(1)求m;
(2)當a>1時,若函數f(x)的圖象與直線l:y=﹣mx+n無公共點,求n的取值范圍.
【答案】
(1)解:∵函數f(x)=loga(ax+1)+mx是偶函數.
∴f(﹣x)=f(x),
即loga(a﹣x+1)﹣mx=loga(ax+1)+mx,
即loga( ![]() )=﹣x=2mx,
)=﹣x=2mx,
解得:m=﹣ ![]()
(2)解:令loga(ax+1)+mx=﹣mx+n,
即n=loga(ax+1)+2mx=loga(ax+1)﹣x,
n′= ![]() ﹣1=
﹣1= ![]() <0恒成立,
<0恒成立,
即n=loga(ax+1)﹣x為減函數,
∵ ![]() →+∞,
→+∞,
![]() →0,
→0,
故n∈(0,+∞),
若函數f(x)的圖象與直線l:y=﹣mx+n無公共點,則n∈(﹣∞,0]
【解析】(1)若函數f(x)=loga(ax+1)+mx是偶函數.則f(﹣x)=f(x),進而可得m的值;(2)令loga(ax+1)+mx=﹣mx+n,即n=loga(ax+1)+2mx=loga(ax+1)﹣x,求出函數的值域,可得答案.


科目:高中數學 來源: 題型:
【題目】如圖,E是矩形ABCD中AD邊上的點,F是CD上的點,AB=AE= ![]() AD=4,現將△ABE沿BE邊折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.
AD=4,現將△ABE沿BE邊折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF. 
(1)求 ![]() 的比值;
的比值;
(2)求二面角E﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知指數函數y=g(x)滿足g(3)=8,又定義域為實數集R的函數f(x)= ![]() 是奇函數.
是奇函數.
(1)討論函數y=f(x)的單調性;
(2)若對任意的t∈R,不等式f(2t﹣3t2)+f(t2﹣k)>0恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和Sn=2an﹣a1 , 且a1 , a2+1,a3成等差數列.
(1)求數列{an}的通項公式;
(2)記數列 ![]() 的前n項和Tn , 求使得
的前n項和Tn , 求使得 ![]() 成立的n的最小值.
成立的n的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 則異面直線BA1與AC1所成的角等于( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}中,a1=2,a2=3,an>0,且滿足an+12﹣an=an+1+an2(n∈N*).
(1)求數列{an}的通項公式;
(2)設 ![]() ,求數列{bn}的前n項和Tn;
,求數列{bn}的前n項和Tn;
(3)設 ![]() (λ為正偶數,n∈N*),是否存在確定λ的值,使得對任意n∈N* , 有Cn+1>Cn恒成立,若存在,求出λ的值,若不存在,說明理由.
(λ為正偶數,n∈N*),是否存在確定λ的值,使得對任意n∈N* , 有Cn+1>Cn恒成立,若存在,求出λ的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為1的正方體中,P是側棱CC1上的一點,CP=m 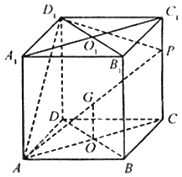
(1)試確定m,使直線AP與平面BDD1B1所成角的正切值為 ![]() ;
;
(2)在線段A1C1上是否存在一個定點Q,使得對任意的m,D1Q在平面APD1上的射影垂直于AP,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知半徑為 ![]() 的圓C,其圓心在射線y=﹣2x(x<0)上,且與直線x+y+1=0相切.
的圓C,其圓心在射線y=﹣2x(x<0)上,且與直線x+y+1=0相切.
(1)求圓C的方程;
(2)從圓C外一點P(x0 , y0))向圓引切線PM,M為切點,O為坐標原點,且有|PM|=|PO|,求△PMC面積的最小值,并求此時點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com