
【題目】已知函數![]() 與
與![]() (其中
(其中![]() )在
)在![]() 上的單調性正好相反,回答下列問題:
上的單調性正好相反,回答下列問題:
(1)對于![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)令![]() ,兩正實數
,兩正實數![]() 、
、![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
【答案】見解析
【解析】(1)因為![]() ,所以
,所以![]() (
(![]() ),
),
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為減函數;
上為減函數;
②當![]() 時,
時,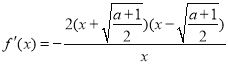 .
.
令![]() ,得
,得![]() ,此時
,此時![]() 在
在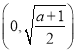 上為增函數;
上為增函數;
令![]() ,得
,得![]() ,此時
,此時![]() 在
在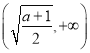 上為減函數;
上為減函數;
又因為![]() ,則
,則![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為增函數,由(1)知,可能與
上為增函數,由(1)知,可能與![]() 單調性相同;
單調性相同;
②當![]() 時,
時,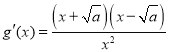 ,
,
令![]() ,得
,得![]() ,此時
,此時![]() 在
在![]() 上為增函數;
上為增函數;
令![]() ,得
,得![]() ,此時
,此時![]() 在
在![]() 上為減函數.
上為減函數.
于是若要![]() 與
與![]() 在
在![]() 上的單調性正好相反,
上的單調性正好相反,
則必須![]() ,解得
,解得![]() .
.
∴![]() ,
,![]() . .............................(4分)
. .............................(4分)
所以,函數![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 上單調遞減;
上單調遞減;
函數![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 上單調遞增.
上單調遞增.
∴在區間![]() 上:
上:
對于函數![]() 有
有![]() ,
,
又![]() ,
,![]()
![]() ,
,
∴![]() .
.
對于函數![]() 有
有![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ..............................(6分)
..............................(6分)
當![]() ,即
,即![]() 時,不等式恒成立;
時,不等式恒成立;
當![]() ,即
,即![]() 時,不等式恒成立需滿足:
時,不等式恒成立需滿足:![]() ,
,
∴![]() .
.
綜上,所求![]() 的范圍為
的范圍為![]()
![]() ..............................(8分)
..............................(8分)
(2)易得![]() ,
,
由![]() ,得
,得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ............................(11分)
............................(11分)
令![]() ,設
,設![]() ,則
,則![]() ,
,
可知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
∴![]() ,
,
∴![]() ...........................(12分)
...........................(12分)
【命題意圖】本題主要考查不等式恒成立問題的求解,導數在研究函數中的應用,意在考查學生的邏輯思維能力和分析問題、解決問題的綜合能力.


科目:高中數學 來源: 題型:
【題目】數列{an}滿足an+1+(﹣1)nan=2n﹣1,則{an}的前60項和為( )
A. 3690 B. 3660 C. 1845 D. 1830
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題
①樣本方差反映的是所有樣本數據與樣本平均值的偏離程度;
②從含有2008個個體的總體中抽取一個容量為100的樣本,現采用系統抽樣方法應先剔除8人,則每個個體被抽到的概率均為![]() ;
;
③從總體中抽取的樣本數據共有m個a,n個b,p個c,則總體的平均數![]() 的估計值為
的估計值為![]() ;
;
④某中學采用系統抽樣方法,從該校高一年級全體800名學生中抽50名學生做牙齒健康檢查,現將800名學生從001到800進行編號,已知從497--512這16個數中取得的學生編號是503,則初始在第1小組00l~016中隨機抽到的學生編號是007.
其中真命題的個數是 _____個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動點![]() 與定點
與定點![]() 的距離和它到定直線
的距離和它到定直線![]() 的距離的比是
的距離的比是![]() ∶
∶![]() ,記點
,記點![]() 的軌跡為
的軌跡為![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)對于定點![]() ,作過點
,作過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() ,
,![]() ,求△
,求△![]() 的內切圓半徑的最大值.
的內切圓半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正四面體ABCD的棱長為2,棱AD與平面α所成的角θ∈[ ![]() ,
, ![]() ],且頂點A在平面α內,B,C,D均在平面α外,則棱BC的中點E到平面α的距離的取值范圍是( )
],且頂點A在平面α內,B,C,D均在平面α外,則棱BC的中點E到平面α的距離的取值范圍是( ) 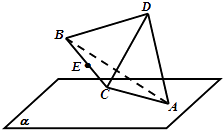
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某校舉行的航天知識競賽中,參與競賽的文科生與理科生人數之比為1:3,且成績分布在[40,100],分數在80以上(含80)的同學獲獎.按文理科用分層抽樣的方法抽取200人的成績作為樣本,并按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組,得到成績的頻率分布直方圖(見下圖).
分組,得到成績的頻率分布直方圖(見下圖).

(1)求![]() 的值,并計算所抽取樣本的平均值
的值,并計算所抽取樣本的平均值![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)填寫下面的2×2列聯表,能否在犯錯誤的概率不超過0.05的前提下認為“獲獎與學生的文理科有關”?
文科生 | 理科生 | 合計 | |
獲獎 | 5 | ||
不獲獎 | |||
合計 | 200 |
附表及公式:
![]()
![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由于渤海海域水污染嚴重,為了獲得第一手的水文資料,潛水員需要潛入水深為60米的水底進行作業,根據經驗,潛水員下潛的平均速度為![]() (米/單位時間),每單位時間消耗氧氣
(米/單位時間),每單位時間消耗氧氣![]() (升),在水底作業10個單位時間,每單位時間消耗氧氣
(升),在水底作業10個單位時間,每單位時間消耗氧氣![]() (升),返回水面的平均速度為
(升),返回水面的平均速度為![]() (米/單位時間),每單位時間消耗氧氣
(米/單位時間),每單位時間消耗氧氣![]() (升),記該潛水員完成此次任務的消耗氧氣總量為
(升),記該潛水員完成此次任務的消耗氧氣總量為![]() (升).
(升).
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)若![]() ,求當下潛速度
,求當下潛速度![]() 取什么值時,消耗氧氣的總量最少.
取什么值時,消耗氧氣的總量最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念,記交通指數為![]() ,其范圍為
,其范圍為![]() ,分為五個級別,
,分為五個級別, ![]() 暢通;
暢通; ![]() 基本暢通;
基本暢通; ![]() 輕度擁堵;
輕度擁堵; ![]() 中度擁堵;
中度擁堵; ![]() 嚴重擁堵.早高峰時段(
嚴重擁堵.早高峰時段(![]() ),從某市交通指揮中心隨機選取了三環以內的50個交通路段,依據其交通指數數據繪制的頻率分布直方圖如圖.
),從某市交通指揮中心隨機選取了三環以內的50個交通路段,依據其交通指數數據繪制的頻率分布直方圖如圖.

(1)這50個路段為中度擁堵的有多少個?
(2)據此估計,早高峰三環以內的三個路段至少有一個是嚴重擁堵的概率是多少?
(3)某人上班路上所用時間若暢通時為20分鐘,基本暢通為30分鐘,輕度擁堵為36分鐘,中度擁堵為42分鐘,嚴重擁堵為60分鐘,求此人所用時間的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com