
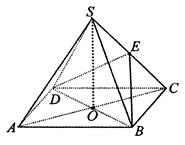
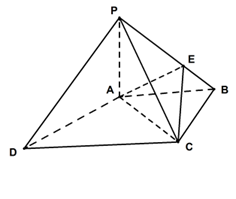
(本題滿分12分)如圖,四棱錐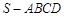 中,底面
中,底面 是邊長為4的正方形,
是邊長為4的正方形,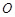 是
是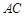 與
與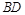 的交點(diǎn),
的交點(diǎn),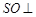 平面
平面 ,
,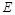 是側(cè)棱
是側(cè)棱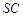 的中點(diǎn),異面直線
的中點(diǎn),異面直線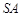 和
和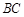 所成角的大小是60
所成角的大小是60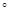 .
.
(Ⅰ)求證:直線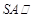 平面
平面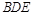 ;
;
(Ⅱ)求直線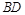 與平面
與平面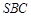 所成角的正弦值.
所成角的正弦值.
(Ⅰ)見解析;(Ⅱ)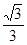 。
。
解析試題分析:(Ⅰ)連結(jié)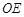 ,……1分
,……1分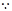 四邊形
四邊形 是正方形,
是正方形, 是
是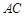 的中點(diǎn),…2分
的中點(diǎn),…2分
又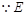 是側(cè)棱
是側(cè)棱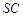 的中點(diǎn),
的中點(diǎn),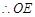 //
//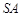 .又
.又 平面
平面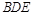 ,
, 平面
平面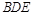 ,
,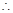 直線
直線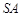 //平面
//平面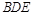 .…………4分
.…………4分
(Ⅱ)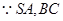 所成角為
所成角為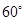 ,
,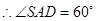 ,
,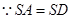
 為等邊三角形
為等邊三角形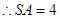 ......5分在
......5分在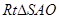 中,
中,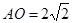 ,
,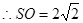 建立如圖空間坐標(biāo)系,
建立如圖空間坐標(biāo)系,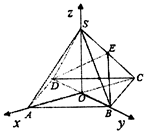
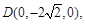
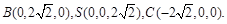
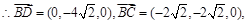
 …………………7分
…………………7分
設(shè)平面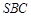 的法向量
的法向量 ,則有
,則有 即
即 解得
解得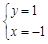
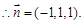 …………9分
…………9分
直線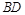 與平面
與平面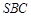 所成角記為
所成角記為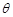 ,則
,則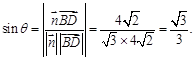 …12分
…12分
考點(diǎn):線面垂直的性質(zhì)定理;異面直線所成的角;直線與平面所成的角;直線與平面平行的判定定理.
點(diǎn)評:本題考查直線與平面平行的證明及直線與平面所成角的正弦值的求法.解題時要認(rèn)真審題,仔細(xì)解答,注意向量法的合理運(yùn)用.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分10分) 如圖,P—ABCD是正四棱錐,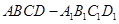 是正方體,其中
是正方體,其中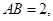
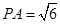
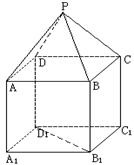
(1)求證: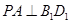 ;
;
(2)求平面PAD與平面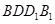 所成的銳二面角
所成的銳二面角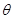 的余弦值;
的余弦值;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分12分)
如圖,棱柱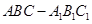 的側(cè)面
的側(cè)面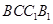 是菱形,
是菱形,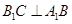
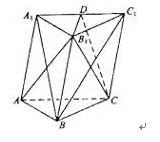
(Ⅰ)證明:平面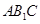
 平面
平面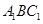 ;
;
(Ⅱ)設(shè) 是
是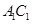 上的點(diǎn),且
上的點(diǎn),且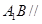 平面
平面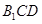 ,求
,求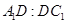 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,已知正方形ABCD的邊長為1,F(xiàn)D⊥平面ABCD,EB⊥平面ABCD,F(xiàn)D=BE=1,M為BC邊上的動點(diǎn).試探究點(diǎn)M的位置,使F—AE—M為直二面角.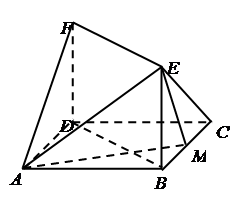
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)如圖,在正方體ABCD-A1B1C1D1中,E、F為棱AD、AB的中點(diǎn).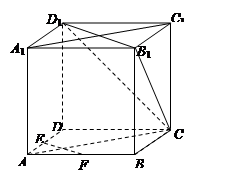
(1)求證:EF ∥平面CB1D1;
(2)求證:平面CAA1C1⊥平面CB1D1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四棱錐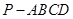 中,
中,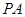 ⊥底面
⊥底面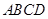 ,底面
,底面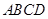 為梯形,
為梯形,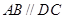 ,
,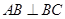 ,
,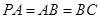 ,點(diǎn)
,點(diǎn)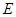 在棱
在棱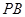 上,且
上,且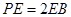 .
.
(1)求證:平面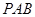 ⊥平面
⊥平面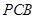 ;
;
(2)求平面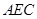 和平面
和平面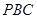 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分12分)
(本題滿分12分)
如圖,已知三棱錐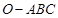 的側(cè)棱
的側(cè)棱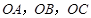 兩兩垂直,
兩兩垂直,
且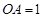 ,
, ,
,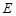 是
是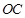 的中點(diǎn)。
的中點(diǎn)。
(1)求異面直線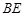 與
與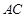 所成角的余弦值;
所成角的余弦值;
(2)求直線BE和平面 的所成角的正弦值。
的所成角的正弦值。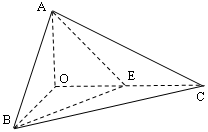
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com