
【題目】如圖,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直線AB,且AB![]() BP
BP![]() 2,AD=AE=1,AE⊥AB,且AE∥BP.
2,AD=AE=1,AE⊥AB,且AE∥BP.

(1)求平面PCD與平面ABPE所成的二面角的余弦值;
(2)線段PD上是否存在一點N,使得直線BN與平面PCD所成角的正弦值等于![]() ?若存在,試確定點N的位置;若不存在,請說明理由.
?若存在,試確定點N的位置;若不存在,請說明理由.
【答案】(1)![]() (2)當點N與點D重合時,直線BN與平面PCD所成角α的正弦值等于
(2)當點N與點D重合時,直線BN與平面PCD所成角α的正弦值等于![]() 。
。
【解析】
試題分析:(1)由面面垂直的性質(zhì)定理可得![]() 平面
平面![]() ,所以直線
,所以直線![]() ,兩兩垂直,以
,兩兩垂直,以![]() 為原點,分別以
為原點,分別以![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,![]()
![]() 為平面
為平面![]() 的一個法向量,利用向量垂直的性質(zhì)列方程組求出平面
的一個法向量,利用向量垂直的性質(zhì)列方程組求出平面![]() 的一個法向量,利用空間向量夾角余弦公式可得結(jié)果;(2)設
的一個法向量,利用空間向量夾角余弦公式可得結(jié)果;(2)設![]() ,
,![]() .由(1)知,平面
.由(1)知,平面![]() 的一個法向量為
的一個法向量為![]() ,利用空間向量夾角余弦公式列方程求解即可.
,利用空間向量夾角余弦公式列方程求解即可.
試題解析:(1)因為平面ABCD⊥平面ABEP,平面ABCD∩平面ABEP![]() AB,BP⊥AB,
AB,BP⊥AB,
所以BP⊥平面ABCD,又AB⊥BC,所以直線BA,BP,BC兩兩垂直,
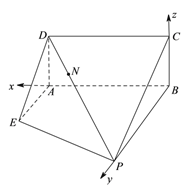
以B為原點,分別以BA,BP,BC為x軸,y軸,z軸建立如圖所示的空間直角坐標系,則P(0,2,0),B(0,0,0),D(![]() 2,0,1),E(2,1,0),C(0,0,1),
2,0,1),E(2,1,0),C(0,0,1),
因為BC⊥平面ABPE,所以![]() 為平面ABPE的一個法向量,
為平面ABPE的一個法向量,
![]() ,設平面PCD的一個法向量為
,設平面PCD的一個法向量為![]() ,
,
則 即
即![]() 令
令![]() ,則
,則![]() ,故
,故![]() ,
,
設平面PCD與平面ABPE所成的二面角為![]() ,則
,則![]() ,
,
顯然![]() ,所以平面PCD與平面ABPE所成二面角的余弦值
,所以平面PCD與平面ABPE所成二面角的余弦值![]() .
.
(2)設線段PD上存在一點N,使得直線BN與平面PCD所成角α的正弦值等于![]() .
.
設![]() ,
,![]() .
.
由(1)知,平面PCD的一個法向量為![]() ,
,
所以![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
當點N與點D重合時,直線BN與平面PCD所成角的正弦值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】某國際性會議紀念章的一特許專營店銷售紀念章,每枚進價為5元,同時每銷售一枚這種紀念章還需向該會議的組織委員會交特許經(jīng)營管理費2元,預計這種紀念章以每枚20元的價格銷售時,該店一年可銷售2000枚,經(jīng)過市場調(diào)研發(fā)現(xiàn),每枚紀念章的銷售價格在每枚20元的基礎上,每減少一元則增加銷售400枚,而每增加一元則減少銷售100枚,現(xiàn)設每枚紀念章的銷售價格為![]() 元(每枚的銷售價格應為正整數(shù)).
元(每枚的銷售價格應為正整數(shù)).
(1)寫出該特許專營店一年內(nèi)銷售這種紀念章所獲得的利潤![]() (元)與每枚紀念章的銷售價格
(元)與每枚紀念章的銷售價格![]() 的函數(shù)關系式;
的函數(shù)關系式;
(2)當每枚紀念章銷售價格![]() 為多少元時,該特許專營店一年內(nèi)利潤
為多少元時,該特許專營店一年內(nèi)利潤![]() (元)最大,并求出這個最大值;
(元)最大,并求出這個最大值;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 滿足
滿足![]() (
(![]() 為常數(shù)),且
為常數(shù)),且![]() =3.
=3.
(1)求實數(shù)![]() 的值,并求出函數(shù)
的值,并求出函數(shù)![]() 的解析式;
的解析式;
(2)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性,并用定義證明你的結(jié)論.
的單調(diào)性,并用定義證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 在點
在點![]() )處的切線方程是
)處的切線方程是![]() .
.
(I)求![]() 的值及函數(shù)
的值及函數(shù)![]() 的最大值
的最大值
(Ⅱ)若實數(shù)![]() 滿足
滿足![]() .
.
(![]() )證明:
)證明:![]() ;
;
(![]() )若
)若![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】分形理論是當今世界十分風靡和活躍的新理論、新學科。其中,把部分與整體以某種方式相似的形體稱為分形。分形是一種具有自相似特性的現(xiàn)象,圖象或者物理過程。標準的自相似分形是數(shù)學上的抽象,迭代生成無限精細的結(jié)構(gòu)。也就是說,在分形中,每一組成部分都在特征上和整體相似,只僅僅是變小了一些而已,謝爾賓斯基三角形就是一種典型的分形,是由波蘭數(shù)學家謝爾賓斯基在1915年提出的,按照如下規(guī)律依次在一個黑色三角形內(nèi)去掉小三角形則當![]() 時,該黑色三角形內(nèi)共去掉( )個小三角形
時,該黑色三角形內(nèi)共去掉( )個小三角形
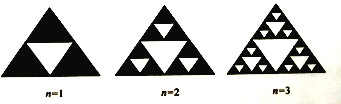
A. 81 B. 121 C. 364 D. 1093
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 過點
過點 ,且兩個焦點的坐標分別為
,且兩個焦點的坐標分別為![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 為
為![]() 上的三個不同的點,
上的三個不同的點, ![]() 為坐標原點,且
為坐標原點,且![]() ,求證:四邊形
,求證:四邊形![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了解人們對“2019年3月在北京召開的第十三屆全國人民代表大會第二次會議和政協(xié)第十三屆全國委員會第二次會議”的關注度,某部門從年齡在15歲到65歲的人群中隨機調(diào)查了100人,并得到如圖所示的年齡頻率分布直方圖,在這100人中關注度非常髙的人數(shù)與年齡的統(tǒng)計結(jié)果如右表所示:

年齡 | 關注度非常高的人數(shù) |
| 15 |
| 5 |
| 15 |
| 23 |
| 17 |
(Ⅰ)由頻率分布直方圖,估計這100人年齡的中位數(shù)和平均數(shù);
(Ⅱ)根據(jù)以上統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表,據(jù)此表,能否在犯錯誤的概率不超過
列聯(lián)表,據(jù)此表,能否在犯錯誤的概率不超過![]() 的前提下,認為以45歲為分界點的不同人群對“兩會”的關注度存在差異?
的前提下,認為以45歲為分界點的不同人群對“兩會”的關注度存在差異?
(Ⅲ)按照分層抽樣的方法從年齡在35歲以下的人中任選六人,再從六人中隨機選兩人,求兩人中恰有一人年齡在25歲以下的概率是多少.
45歲以下 | 45歲以上 | 總計 | |
非常髙 | |||
一般 | |||
總計 |
參考數(shù)據(jù):
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() ,試討論函數(shù)
,試討論函數(shù)![]() 零點的個數(shù);
零點的個數(shù);
(3)在(2)的條件下,若![]() 有兩個零點
有兩個零點![]() ,
,![]()
![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com