
【題目】已知在數(shù)列{an}中,Sn為其前n項和,若an>0,且4Sn=an2+2an+1(n∈N*),數(shù)列{bn}為等比數(shù)列,公比q>1,b1=a1,且2b2,b4,3b3成等差數(shù)列.
(1)求{an}與{bn}的通項公式;
(2)令cn=![]() ,若{cn}的前項和為Tn,求證:Tn<6.
,若{cn}的前項和為Tn,求證:Tn<6.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】試題分析:(1)先根據(jù)得![]() 遞推關(guān)系,化簡得
遞推關(guān)系,化簡得![]() ,根據(jù)等差數(shù)列定義及通項公式得
,根據(jù)等差數(shù)列定義及通項公式得![]() ,由待定系數(shù)法求數(shù)列{bn}公比為2,再根據(jù)等比數(shù)列通項公式求bn=2n-1(2)利用錯位相減法求和
,由待定系數(shù)法求數(shù)列{bn}公比為2,再根據(jù)等比數(shù)列通項公式求bn=2n-1(2)利用錯位相減法求和![]() ,再證結(jié)論;利用錯位相減法求和時,注意相減時項的符號變化,中間部分利用等比數(shù)列求和時注意項數(shù),最后要除以
,再證結(jié)論;利用錯位相減法求和時,注意相減時項的符號變化,中間部分利用等比數(shù)列求和時注意項數(shù),最后要除以![]()
試題解析:解:(1)由4Sn=an2+2an+1(n∈N*),n=1時,4a1=![]() +2a1+1,解得a1=1.
+2a1+1,解得a1=1.
n≥2時,4Sn-1=![]() +2an-1+1,相減可得:4an=
+2an-1+1,相減可得:4an=![]() -
-![]() ,化為:(an+an-1)(an-an-1-2)=0,
,化為:(an+an-1)(an-an-1-2)=0,
又an>0,∴an-an-1-2=0,即an-an-1=2,
∴數(shù)列{an}是等差數(shù)列,公差為2. ∴an=1+2(n-1)=2n-1.
b1=a1=1,∵2b2,b4,3b3成等差數(shù)列.
∴2b4=2b2+3b3.∴![]() =2b2+3b2q,化為:2q2-3q-2=0,q>1,解得q=2.
=2b2+3b2q,化為:2q2-3q-2=0,q>1,解得q=2.
∴bn=2n-1.
(2)證明:cn=![]() =
=![]() .
.
{cn}的前項和為Tn=1+![]() +…+
+…+![]() ,
, ![]() Tn=
Tn=![]() +…+
+…+![]() +
+![]() ,
,
∴![]() Tn=1+2
Tn=1+2![]() -
-![]() =1+2×
=1+2×![]() -
-![]() ,
,
∴Tn=6-![]() <6.
<6.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() 是自然對數(shù)的底數(shù)),曲線
是自然對數(shù)的底數(shù)),曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸平行.
軸平行.
(1)求![]() 的值;
的值;
(2)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)設(shè)![]() ,其中
,其中![]() 為
為![]() 的導(dǎo)函數(shù).證明:對任意
的導(dǎo)函數(shù).證明:對任意![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正四面體![]() 的頂點
的頂點![]() 、
、![]() 、
、![]() 分別在兩兩垂直的三條射線
分別在兩兩垂直的三條射線![]() ,
, ![]() ,
, ![]() 上,則在下列命題中,錯誤的是( )
上,則在下列命題中,錯誤的是( )
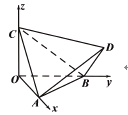
A. ![]() 是正三棱錐
是正三棱錐
B. 直線![]() 與平面
與平面![]() 相交
相交
C. 直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]()
D. 異面直線![]() 和
和![]() 所成角是
所成角是![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() .
.
(1)若直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,當(dāng)
,當(dāng)![]() 時,求
時,求![]() 的值.
的值.
(2)若![]() 是直線
是直線![]() 上的動點,過
上的動點,過![]() 作圓
作圓![]() 的兩條切線
的兩條切線![]() ,切點為
,切點為![]() ,探究:直線
,探究:直線![]() 是否過定點;
是否過定點;
(3)若![]() 為圓
為圓![]() 的兩條相互垂直的弦,垂足為
的兩條相互垂直的弦,垂足為 ,求四邊形
,求四邊形![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某同學(xué)用“五點法”畫函數(shù)f(x)=Asin(ωx+φ)(ω>0,|φ|<![]() )在某一個周期內(nèi)的圖象時,列表并填入了部分?jǐn)?shù)據(jù),如表:
)在某一個周期內(nèi)的圖象時,列表并填入了部分?jǐn)?shù)據(jù),如表:
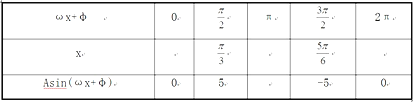
(1)請將上表數(shù)據(jù)補充完整,并直接寫出函數(shù)f(x)的解析式.
(2)將y=f(x)圖象上所有點向左平行移動θ(θ>0)個單位長度,得到y(tǒng)=g(x)的圖象.若y=g(x)圖象的一個對稱中心為![]() ,求θ的最小值.
,求θ的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在四棱錐P-ABCD中,底面ABCD是棱長為2的正方形,側(cè)面PAD為正三角形,且面PAD⊥面ABCD,E、F分別為棱AB、PC的中點.
(1)求證:EF∥平面PAD;
(2)求三棱錐B-EFC的體積;
(3)求二面角P-EC-D的正切值.
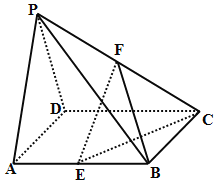
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校學(xué)生社團(tuán)心理學(xué)研究小組在對學(xué)生上課注意力集中情況的調(diào)查研究中,發(fā)現(xiàn)其在40分鐘的一節(jié)課中,注意力指數(shù)![]() 與聽課時間
與聽課時間![]() (單位:分鐘)之間的關(guān)系滿足如圖所示的曲線.當(dāng)
(單位:分鐘)之間的關(guān)系滿足如圖所示的曲線.當(dāng)![]() 時,曲線是二次函數(shù)圖象的一部分,當(dāng)
時,曲線是二次函數(shù)圖象的一部分,當(dāng)![]() 時,曲線是函數(shù)
時,曲線是函數(shù)![]() 圖象的一部分.根據(jù)專家研究,當(dāng)注意力指數(shù)
圖象的一部分.根據(jù)專家研究,當(dāng)注意力指數(shù)![]() 大于80時學(xué)習(xí)效果最佳.
大于80時學(xué)習(xí)效果最佳.
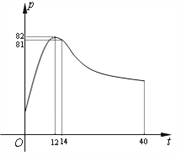
(1)試求![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)教師在什么時段內(nèi)安排核心內(nèi)容,能使得學(xué)生學(xué)習(xí)效果最佳?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC是銳角三角形,cos22A+sin2A=1.
(Ⅰ)求角A;
(Ⅱ)若BC=1,B=x,求△ABC的周長f(x)的單調(diào)區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() ,
,![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若對滿足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() 對一切
對一切![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com