
【題目】函數(shù)![]() ,
, ![]() (
(![]() 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù), ![]() ).
).
(Ⅰ)求證: ![]() ;
;
(Ⅱ)已知![]() 表示不超過
表示不超過![]() 的最大整數(shù),如
的最大整數(shù),如![]() ,
, ![]() ,若對任意
,若對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:
(Ⅰ)首先得出![]() ,求出導(dǎo)函數(shù)
,求出導(dǎo)函數(shù)![]() ,由
,由![]() 確定增區(qū)間,
確定增區(qū)間, ![]() 確定減區(qū)間,從而確定出
確定減區(qū)間,從而確定出![]() 的最小值為
的最小值為![]() ,而
,而![]() ,由此不等式得證;
,由此不等式得證;
(Ⅱ)此問題首先進(jìn)行轉(zhuǎn)化,當(dāng)![]() 時(shí),
時(shí), ![]() 的最小值為
的最小值為![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() 的最小值為
的最小值為![]() ,依題意有
,依題意有![]() ,而由(Ⅰ)知
,而由(Ⅰ)知![]() =0,因此有
=0,因此有![]() ,下面就是求出
,下面就是求出![]() 的最小值,即可得出
的最小值,即可得出![]() 的范圍,為此可求
的范圍,為此可求![]() 的導(dǎo)數(shù)
的導(dǎo)數(shù)![]() .為了確定
.為了確定![]() 的正負(fù),令
的正負(fù),令![]() ,再求導(dǎo)
,再求導(dǎo)![]() ,
,
而當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() ,
, ![]() 在
在![]() 上是增函數(shù),所以
上是增函數(shù),所以![]() .下面對
.下面對![]() 按正負(fù)分類討論:
按正負(fù)分類討論:
A①![]() ,
, ![]() 在
在![]() 上是增函數(shù),最小值為
上是增函數(shù),最小值為![]() ;②
;②![]() ,即
,即![]() 時(shí),因?yàn)?/span>
時(shí),因?yàn)?/span>![]() 在
在![]() 上是增函數(shù),且
上是增函數(shù),且![]() ,因此
,因此![]() 在
在![]() 上有一個(gè)零點(diǎn),記為
上有一個(gè)零點(diǎn),記為![]() ,
,
![]() ,即
,即![]() ,這樣有當(dāng)
,這樣有當(dāng)![]() 時(shí),
時(shí), ![]() ,即
,即![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí), ![]() ,即
,即![]() ,所以,
,所以, ![]() 在
在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù),所以
上是增函數(shù),所以![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .由
.由![]() ,可令
,可令![]() ,由此求出
,由此求出![]() 的范圍,即此時(shí)
的范圍,即此時(shí)![]() 的范圍,綜合以上兩點(diǎn)可得.
的范圍,綜合以上兩點(diǎn)可得.
試題解析:
(Ⅰ)![]() (
(![]() ).
).
當(dāng)![]() 時(shí),
時(shí), ![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() ,
,
即![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以,當(dāng)![]() 時(shí),
時(shí), ![]() 取得最小值,最小值為
取得最小值,最小值為![]() ,
,
所以![]() ,
,
又![]() ,且當(dāng)
,且當(dāng)![]() 時(shí)等號成立,
時(shí)等號成立,
所以, ![]() .
.
(Ⅱ)記當(dāng)![]() 時(shí),
時(shí), ![]() 的最小值為
的最小值為![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() 的最小值為
的最小值為![]() ,
,
依題意有![]() ,
,
由(Ⅰ)知![]() ,所以
,所以![]() ,則有
,則有![]() ,
,
![]() .
.
令![]() ,
, ![]() ,
,
而當(dāng)![]() 時(shí),
時(shí), ![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上是增函數(shù),所以
上是增函數(shù),所以![]() .
.
①當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() 恒成立,即
恒成立,即![]() ,
,
所以![]() 在
在![]() 上是增函數(shù),所以
上是增函數(shù),所以![]() ,
,
依題意有![]() ,解得
,解得![]() ,
,
所以![]() .
.
②當(dāng)![]() ,即
,即![]() 時(shí),因?yàn)?/span>
時(shí),因?yàn)?/span>![]() 在
在![]() 上是增函數(shù),且
上是增函數(shù),且![]() ,
,
若![]() ,即
,即![]() ,則
,則![]() ,
,
所以![]() ,使得
,使得![]() ,即
,即![]() ,
,
且當(dāng)![]() 時(shí),
時(shí), ![]() ,即
,即![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí), ![]() ,即
,即![]() ,
,
所以, ![]() 在
在![]() 上是減函數(shù),在
上是減函數(shù),在![]() 上是增函數(shù),
上是增函數(shù),
所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
由![]() ,可令
,可令![]() ,
,
![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() ,所以
,所以![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
所以當(dāng)![]() 時(shí),
時(shí), ![]() ,即
,即![]() ,
,
所以![]() .
.
綜上,所求實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


 浙大優(yōu)學(xué)小學(xué)年級銜接捷徑浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接捷徑浙江大學(xué)出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,(1)已知a=![]() ,b=
,b=![]() ,B=45°,求A、C、c;
,B=45°,求A、C、c;
(2)已知sin A∶sin B∶sin C=(![]() +1)∶(
+1)∶(![]() -1)∶
-1)∶![]() ,求最大角.
,求最大角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C經(jīng)過點(diǎn)![]() ,且圓心
,且圓心![]() 在直線
在直線![]() 上,又直線
上,又直線![]() 與圓C交于P,Q兩點(diǎn).
與圓C交于P,Q兩點(diǎn).
(1)求圓C的方程;
(2)若![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(3)過點(diǎn)![]() 作直線
作直線![]() ,且
,且![]() 交圓C于M,N兩點(diǎn),求四邊形
交圓C于M,N兩點(diǎn),求四邊形![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在矩形ABCD中,邊AB、AD的長分別為2,1,若M,N分別是邊BC、CD上的點(diǎn),且滿足 ![]() =
= ![]() =λ.
=λ. 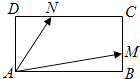
(1)當(dāng)λ= ![]() 時(shí),求向量
時(shí),求向量 ![]() 和
和 ![]() 夾角的余弦值;
夾角的余弦值;
(2)求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某職稱晉級評定機(jī)構(gòu)對參加某次專業(yè)技術(shù)考試的100人的成績進(jìn)行了統(tǒng)計(jì),繪制了頻率分布直方圖(如圖所示),規(guī)定80分及以上者晉級成功,否則晉級失敗(滿分為100分).

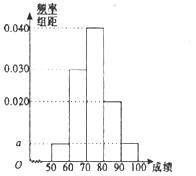
(1)求圖中![]() 的值;
的值;
(2)估計(jì)該次考試的平均分![]() (同一組中的數(shù)據(jù)用該組的區(qū)間中點(diǎn)值代表);
(同一組中的數(shù)據(jù)用該組的區(qū)間中點(diǎn)值代表);
(3)根據(jù)已知條件完成下面![]() 列聯(lián)表,并判斷能否有85%的把握認(rèn)為“晉級成功”與性別有關(guān)?
列聯(lián)表,并判斷能否有85%的把握認(rèn)為“晉級成功”與性別有關(guān)?
(參考公式: 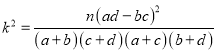 ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】據(jù)統(tǒng)計(jì),某物流公司每天的業(yè)務(wù)中,從甲地到乙地的可配送的貨物量![]() 的頻率分布直方圖,如圖所示,將頻率視為概率,回答以下問題.
的頻率分布直方圖,如圖所示,將頻率視為概率,回答以下問題.
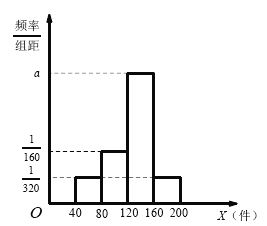
(1)求該物流公司每天從甲地到乙地平均可配送的貨物量;
(2)該物流公司擬購置貨車專門運(yùn)營從甲地到乙地的貨物,一輛貨車每天只能運(yùn)營一趟,每輛車每
趟最多只能裝載40 件貨物,滿載發(fā)車,否則不發(fā)車。若發(fā)車,則每輛車每趟可獲利1000 元;若未發(fā)車,
則每輛車每天平均虧損200 元。為使該物流公司此項(xiàng)業(yè)務(wù)的營業(yè)利潤最大,該物流公司應(yīng)該購置幾輛貨
車?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為拋物線
為拋物線![]() 的焦點(diǎn),過
的焦點(diǎn),過![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn), ![]() 為
為![]() 中點(diǎn),點(diǎn)
中點(diǎn),點(diǎn)![]() 到
到![]() 軸的距離為
軸的距離為![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)過![]() 分別作
分別作![]() 的兩條切線
的兩條切線![]() ,
, ![]() .請選擇
.請選擇![]() 軸中的一條,比較
軸中的一條,比較![]() 到該軸的距離.
到該軸的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示, ![]() 矩形
矩形![]() 所在的平面,
所在的平面, ![]() 分別是
分別是![]() 的中點(diǎn).
的中點(diǎn).
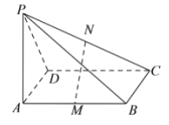
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證: ![]() .
.
(3)當(dāng)![]() 滿足什么條件時(shí),能使
滿足什么條件時(shí),能使![]() 平面
平面![]() 成立?并證明你的結(jié)論.
成立?并證明你的結(jié)論.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com