Question

【題目】設各項均為正數(shù)的數(shù)列的前項和為，滿足，且，公比大于1的等比數(shù)列滿足， .

（1）求證數(shù)列是等差數(shù)列，并求其通項公式；

（2）若，求數(shù)列的前項和；

（3）在（2）的條件下，若對一切正整數(shù)恒成立，求實數(shù)的取值

Answer 1

【答案】（1）；（2）；（3）.

【解析】試題分析：（1）由與的關系，可求出，利用等差數(shù)列定義即可證明；（2）根據(jù)通項是等差數(shù)列與等比數(shù)列相乘的特點，用錯位相減法求和；（3）可證明數(shù)列是單調遞減數(shù)列，故可轉化為恒成立，利用二次不等式恒成立的方法即可求解.

試題解析：（1）當時， ， ，

，所以， .

因為當時， 是公差的等差數(shù)列，

， ，

則是首項，公差的等差數(shù)列，

所以數(shù)列的通項公式為.

（2）由題意得， ；

則前項和 ；

；

相減可得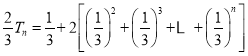

；

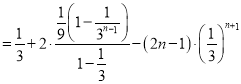化簡可得前項和；

（3）對一切正整數(shù)恒成立，

由 ，

可得數(shù)列單調遞減，即有最大值為，

則，解得或.

即實數(shù)的取值范圍為.