
【題目】已知拋物線C:y2=2x,過點(2,0)的直線l交C與A,B兩點,圓M是以線段AB為直徑的圓.
(Ⅰ)證明:坐標原點O在圓M上;
(Ⅱ)設圓M過點P(4,﹣2),求直線l與圓M的方程.
【答案】解:方法一:證明:(Ⅰ)當直線l的斜率不存在時,則A(2,2),B(2,﹣2),
則 ![]() =(2,2),
=(2,2), ![]() =(2,﹣2),則
=(2,﹣2),則 ![]()
![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() ,
,
則坐標原點O在圓M上;
當直線l的斜率存在,設直線l的方程y=k(x﹣2),設A(x1 , y1),B(x2 , y2),![]() ,整理得:k2x2﹣(4k2+2)x+4k2=0,
,整理得:k2x2﹣(4k2+2)x+4k2=0,
則x1x2=4,4x1x2=y12y22=(y1y2)2 , 由y1y2<0,
則y1y2=﹣4,
由 ![]()
![]() =x1x2+y1y2=0,
=x1x2+y1y2=0,
則 ![]() ⊥
⊥ ![]() ,則坐標原點O在圓M上,
,則坐標原點O在圓M上,
綜上可知:坐標原點O在圓M上;
方法二:設直線l的方程x=my+2,![]() ,整理得:y2﹣2my﹣4=0,設A(x1 , y1),B(x2 , y2),
,整理得:y2﹣2my﹣4=0,設A(x1 , y1),B(x2 , y2),
則y1y2=﹣4,
則(y1y2)2=4x1x2 , 則x1x2=4,則 ![]()
![]() =x1x2+y1y2=0,
=x1x2+y1y2=0,
則 ![]() ⊥
⊥ ![]() ,則坐標原點O在圓M上,
,則坐標原點O在圓M上,
∴坐標原點O在圓M上;
(Ⅱ)由(Ⅰ)可知:x1x2=4,x1+x2= ![]() ,y1+y2=
,y1+y2= ![]() ,y1y2=﹣4,
,y1y2=﹣4,
圓M過點P(4,﹣2),則 ![]() =(4﹣x1 , ﹣2﹣y1),
=(4﹣x1 , ﹣2﹣y1), ![]() =(4﹣x2/span> , ﹣2﹣y2),
=(4﹣x2/span> , ﹣2﹣y2),
由 ![]()
![]() =0,則(4﹣x1)(4﹣x2)+(﹣2﹣y1)(﹣2﹣y2)=0,
=0,則(4﹣x1)(4﹣x2)+(﹣2﹣y1)(﹣2﹣y2)=0,
整理得:k2+k﹣2=0,解得:k=﹣2,k=1,
當k=﹣2時,直線l的方程為y=﹣2x+4,
則x1+x2= ![]() ,y1+y2=﹣1,
,y1+y2=﹣1,
則M( ![]() ,﹣
,﹣ ![]() ),半徑為r=丨MP丨=
),半徑為r=丨MP丨= ![]() =
= ![]() ,
,
∴圓M的方程(x﹣ ![]() )2+(y+
)2+(y+ ![]() )2=
)2= ![]() .
.
當直線斜率k=1時,直線l的方程為y=x﹣2,
同理求得M(3,1),則半徑為r=丨MP丨= ![]() ,
,
∴圓M的方程為(x﹣3)2+(y﹣1)2=10,
綜上可知:直線l的方程為y=﹣2x+4,圓M的方程(x﹣ ![]() )2+(y+
)2+(y+ ![]() )2=
)2= ![]()
或直線l的方程為y=x﹣2,圓M的方程為(x﹣3)2+(y﹣1)2=10.
【解析】(Ⅰ)方法一:分類討論,當直線斜率不存在時,求得A和B的坐標,由 ![]()
![]() =0,則坐標原點O在圓M上;當直線l斜率存在,代入拋物線方程,利用韋達定理及向量數量積的可得
=0,則坐標原點O在圓M上;當直線l斜率存在,代入拋物線方程,利用韋達定理及向量數量積的可得 ![]()
![]() =0,則坐標原點O在圓M上;
=0,則坐標原點O在圓M上;
方法二:設直線l的方程x=my+2,代入橢圓方程,利用韋達定理及向量數量積的坐標運算,即可求得 ![]()
![]() =0,則坐標原點O在圓M上;
=0,則坐標原點O在圓M上;
(Ⅱ)由題意可知: ![]()
![]() =0,根據向量數量積的坐標運算,即可求得k的值,求得M點坐標,則半徑r=丨MP丨,即可求得圓的方程.
=0,根據向量數量積的坐標運算,即可求得k的值,求得M點坐標,則半徑r=丨MP丨,即可求得圓的方程.
【考點精析】本題主要考查了點斜式方程和斜截式方程的相關知識點,需要掌握直線的點斜式方程:直線![]() 經過點
經過點![]() ,且斜率為
,且斜率為![]() 則:
則:![]() ;直線的斜截式方程:已知直線
;直線的斜截式方程:已知直線![]() 的斜率為
的斜率為![]() ,且與
,且與![]() 軸的交點為
軸的交點為![]() 則:
則:![]() 才能正確解答此題.
才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】某縣教育局為了檢查本縣甲、乙兩所學校的學生對安全知識的學習情況,在這兩所學校進行了安全知識測試,隨機在這兩所學校各抽取20名學生的考試成績作為樣本,成績大于或等于80分的為優秀,否則為不優秀,統計結果如下圖:


甲校 乙校
(1)從乙校成績優秀的學生中任選兩名,求這兩名學生的成績恰有一個落在![]() 內的概率;
內的概率;
(2)由以上數據完成下面列聯表,并回答能否在犯錯的概率不超過0.1的前提下認為學生的成績與兩所學校的選擇有關。
甲校 | 乙校 | 總計 | |
優秀 | |||
不優秀 | |||
總計 |
![]()
參考數據 | P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | span>3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,橢圓E: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,焦距為2.(14分)
,焦距為2.(14分)
(Ⅰ)求橢圓E的方程.
(Ⅱ)如圖,該直線l:y=k1x﹣ ![]() 交橢圓E于A,B兩點,C是橢圓E上的一點,直線OC的斜率為k2 , 且看k1k2=
交橢圓E于A,B兩點,C是橢圓E上的一點,直線OC的斜率為k2 , 且看k1k2= ![]() ,M是線段OC延長線上一點,且|MC|:|AB|=2:3,⊙M的半徑為|MC|,OS,OT是⊙M的兩條切線,切點分別為S,T,求∠SOT的最大值,并求取得最大值時直線l的斜率.
,M是線段OC延長線上一點,且|MC|:|AB|=2:3,⊙M的半徑為|MC|,OS,OT是⊙M的兩條切線,切點分別為S,T,求∠SOT的最大值,并求取得最大值時直線l的斜率.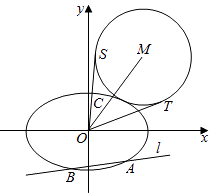
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】校運動會高二理三個班級的3名同學報名參加鉛球、跳高、三級跳遠3個運動項目,每名同學都可以從3個運動項目中隨機選擇一個,且每個人的選擇相互獨立.
(1)求3名同學恰好選擇了2個不同運動項目的概率;
(Ⅱ)設選擇跳高的人數為![]() 試求
試求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】幾位大學生響應國家的創業號召,開發了一款應用軟件.為激發大家學習數學的興趣,他們推出了“解數學題獲取軟件激活碼”的活動.這款軟件的激活碼為下面數學問題的答案:已知數列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一項是20 , 接下來的兩項是20 , 21 , 再接下來的三項是20 , 21 , 22 , 依此類推.求滿足如下條件的最小整數N:N>100且該數列的前N項和為2的整數冪.那么該款軟件的激活碼是( )
A.440
B.330
C.220
D.110
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在矩形ABCD中,AB=1,AD=2,動點P在以點C為圓心且與BD相切的圓上.若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,則λ+μ的最大值為( )
,則λ+μ的最大值為( )
A.3
B.2 ![]()
C.![]()
D.2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com