
【題目】已如長方形![]() 中,
中,![]() ,M為
,M為![]() 的中點,將
的中點,將![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,
,
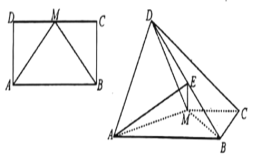
(1)求證:![]() ;
;
(2)若點![]() 是線段
是線段![]() 上的中點,求三棱錐
上的中點,求三棱錐![]() 與四棱錐
與四棱錐![]() 的體積的比值 .
的體積的比值 .
 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:
【題目】一種作圖工具如圖1所示.![]() 是滑槽
是滑槽![]() 的中點,短桿
的中點,短桿![]() 可繞
可繞![]() 轉動,長桿
轉動,長桿![]() 通過
通過![]() 處鉸鏈與
處鉸鏈與![]() 連接,
連接,![]() 上的栓子
上的栓子![]() 可沿滑槽AB滑動,且
可沿滑槽AB滑動,且![]() ,
,![]() .當栓子
.當栓子![]() 在滑槽AB內作往復運動時,帶動
在滑槽AB內作往復運動時,帶動![]() 繞
繞![]() 轉動一周(
轉動一周(![]() 不動時,
不動時,![]() 也不動),
也不動),![]() 處的筆尖畫出的曲線記為
處的筆尖畫出的曲線記為![]() .以
.以![]() 為原點,
為原點,![]() 所在的直線為
所在的直線為![]() 軸建立如圖2所示的平面直角坐標系.
軸建立如圖2所示的平面直角坐標系.
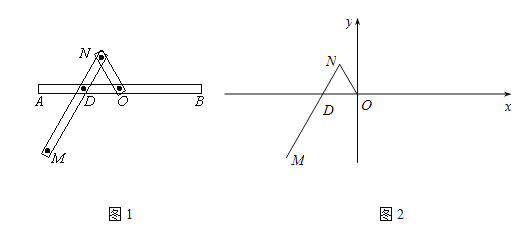
(Ⅰ)求曲線C的方程;
(Ⅱ)設動直線![]() 與兩定直線
與兩定直線![]() 和
和![]() 分別交于
分別交于![]() 兩點.若直線
兩點.若直線![]() 總與曲線
總與曲線![]() 有且只有一個公共點,試探究:
有且只有一個公共點,試探究:![]() 的面積是否存在最小值?若存在,求出該最小值;若不存在,說明理由.
的面積是否存在最小值?若存在,求出該最小值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公差為正數的等差數列,數列
是公差為正數的等差數列,數列![]() 為等比數列,且
為等比數列,且![]() ,
,![]() ,
,![]() .
.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)設數列![]() 是由所有
是由所有![]() 的項,且
的項,且![]() 的項組成的數列,且原項數先后順序保持不變,求數列
的項組成的數列,且原項數先后順序保持不變,求數列![]() 的前2019項的和
的前2019項的和![]() ;
;
(3)對任意給定的![]() 是否存在
是否存在![]() 使
使![]() 成等差數列?若存在,用
成等差數列?若存在,用![]() 分別表示
分別表示![]() 和
和![]() (只要寫出一組即可);若不存在,請說明理由.
(只要寫出一組即可);若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() ,過點
,過點![]() 的直線
的直線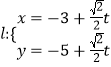 (
(![]() 為參數)與曲線
為參數)與曲線![]() 相交于點
相交于點![]() ,
,![]() 兩點.
兩點.
(1)求曲線![]() 的平面直角坐標系方程和直線
的平面直角坐標系方程和直線![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(導學號:05856331)
甲、乙兩家快餐店對某日7個時段的光顧的客人人數進行統計并繪制莖葉圖如下圖所示(下面簡稱甲數據、乙數據),且乙數據的眾數為17,甲數據的平均數比乙數據平均數少2.
(Ⅰ)求a,b的值,并計算乙數據的方差;
(Ⅱ)現從乙數據中不大于16的數據中隨機抽取兩個,求至少有一個數據小于10的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓的方程為(x-1)2+(y-1)2=9,P(2,2)是該圓內一點,過點P的最長弦和最短弦分別為AC和BD,則四邊形ABCD的面積是______ .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的質量指標值.由測量結果得到如圖所示的頻率分布直方圖,質量指標值落在區間[55,65),[65,75),[75,85]內的頻率之比為4∶2∶1.
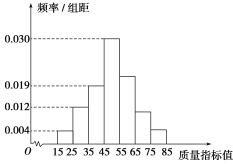
(1)求這些產品質量指標值落在區間[75,85]內的概率;
(2)若將頻率視為概率,從該企業生產的這種產品中隨機抽取3件,記這3件產品中質量指標值位于區間[45,75)內的產品件數為X,求X的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖一是美麗的“勾股樹”,它是一個直角三角形分別以它的每一邊向外作正方形而得到.圖二是第1代“勾股樹”,重復圖二的作法,得到圖三為第2代“勾股樹”,以此類推,已知最大的正方形面積為1,則第![]() 代“勾股樹”所有正方形的個數與面積的和分別為( )
代“勾股樹”所有正方形的個數與面積的和分別為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,若滿足
,若滿足![]() ,則稱函數
,則稱函數![]() 為“
為“![]() 型函數”.
型函數”.
(1)判斷函數![]() 和
和![]() 是否為“
是否為“![]() 型函數”,并說明理由;
型函數”,并說明理由;
(2)設函數![]() ,記
,記![]() 為函數
為函數![]() 的導函數.
的導函數.
①若函數![]() 的最小值為1,求
的最小值為1,求![]() 的值;
的值;
②若函數![]() 為“
為“![]() 型函數”,求
型函數”,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com