已知數(shù)列
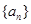
的前
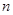
項和為
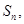
且
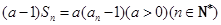
.
(1)求證數(shù)列
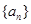
是等比數(shù)列,并求其通項公式
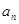
;
(2)已知集合
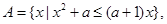
問是否存在實數(shù)
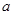
,使得對于任意的
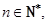
都有
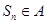
? 若存在,求出
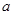
的取值范圍;若不存在,說明理由.
(1)
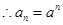
;(2)
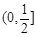
。
(1)當n=1時可先求出a
1.
當n>1時,
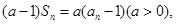
得
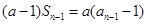
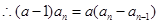
,變形得
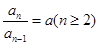
從而可得數(shù)列
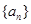
是等比數(shù)列,進而可求出其通項公式.
(2)要分a=1和a>1和0<a<1三種情況分別研究集合A,再研究是否滿足題目條件.
(1)當
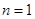
時,
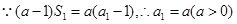
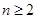
時,由
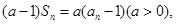
得
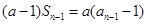
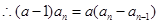
,變形得
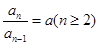
故
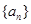
是以
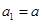
為首項,公比為
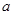
的等比數(shù)列,
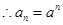
---5分
(2)①當
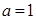
時,
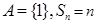
, 只有
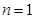
時,

, 所以
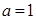
不合題意 ----7分
②當

時,
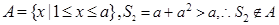
-----9分
③當
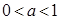
時,
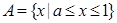
,
而
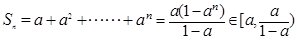
, 對任意
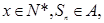


綜上,a的取值范圍是
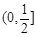
-------------12分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
設關于x的一元二次方程
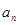
x
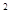
-

x+1=0(n∈N)有兩根α和β,且滿足6α-2αβ+6β=3.
(1)試用
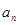
表示a
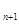
;

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
.已知數(shù)列{an}滿足a1=1,a2=r(r>0),數(shù)列{bn}是公比為q的等比數(shù)列(q>0),bn=anan+1,cn=a2n-1+a2n,求cn。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
等比數(shù)列

中,
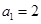
,
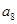
=4,函數(shù)

,則
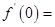
( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設正項等比數(shù)列{
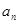
}的前n項和為
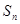
,且
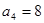
,
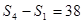
, 則數(shù)列{
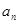
}的公比等于
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設數(shù)列
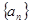
、
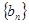
滿足
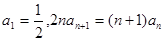
,且
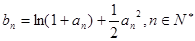
.
(1)求數(shù)列
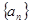
的通項公式;
(2)對一切
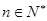
,證明
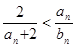
成立;
(3)記數(shù)列
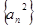
、
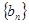
的前
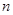
項和分別是
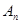
、
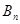
,證明:
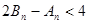
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知等比數(shù)列{an}滿足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),則當n≥1時,log2a1+log2a3+…+log2a2n-1=( )
A(n-1)2 B (n+1)2 C n2 D n2-1
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題14分,計入總分)
已知數(shù)列

滿足:
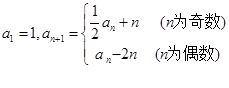
⑴求

;
⑵當

時,求
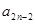
與
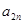
的關系式,并求數(shù)列

中偶數(shù)項的通項公式;
⑶求數(shù)列

前100項中所有奇數(shù)項的和.
查看答案和解析>>

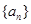 的前
的前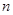 項和為
項和為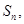 且
且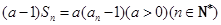 .
.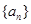 是等比數(shù)列,并求其通項公式
是等比數(shù)列,并求其通項公式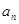 ;
;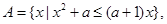 問是否存在實數(shù)
問是否存在實數(shù)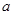 ,使得對于任意的
,使得對于任意的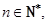 都有
都有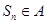 ? 若存在,求出
? 若存在,求出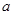 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由. 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案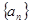 、
、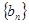 滿足
滿足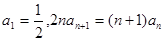 ,且
,且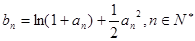 .
.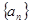 的通項公式;
的通項公式;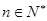 ,證明
,證明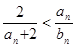 成立;
成立;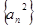 、
、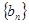 的前
的前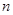 項和分別是
項和分別是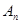 、
、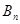 ,證明:
,證明: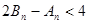 .
. 滿足:
滿足: 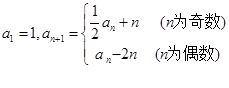
 ;
;  時,求
時,求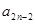 與
與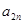 的關系式,并求數(shù)列
的關系式,并求數(shù)列 中偶數(shù)項的通項公式;
中偶數(shù)項的通項公式; 前100項中所有奇數(shù)項的和.
前100項中所有奇數(shù)項的和.