
【題目】等腰直角三角形![]() 中,
中,![]() ,點
,點![]() 在邊
在邊![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
于![]() ,如圖①.將
,如圖①.將![]() 沿
沿![]() 折起,使
折起,使![]() 到達
到達![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,連接
,連接![]() ,
,![]() ,如圖②.
,如圖②.
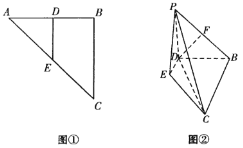
(Ⅰ)若![]() 為
為![]() 的中點,
的中點,![]() ,求證:
,求證:![]() ;
;
(Ⅱ)若![]() ,當三棱錐
,當三棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的余弦值.
的余弦值.
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,從流水線上隨機抽取100件產品,統計其質量指標值并繪制頻率分布直方圖(如圖):
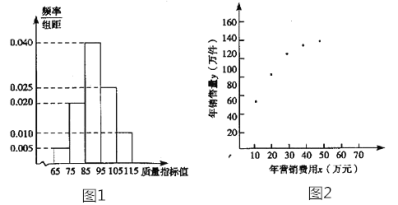
規定產品的質量指標值在![]() 的為劣質品,在
的為劣質品,在![]() 的為優等品,在
的為優等品,在![]() 的為特優品,銷售時劣質品每件虧損1元,優等品每件盈利3元,特優品每件盈利5元.以這100 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
的為特優品,銷售時劣質品每件虧損1元,優等品每件盈利3元,特優品每件盈利5元.以這100 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
(1)求每件產品的平均銷售利潤;
(2)該企業為了解年營銷費用![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:萬件)的影響,對近5年年營銷費用
(單位:萬件)的影響,對近5年年營銷費用![]() 和年銷售量
和年銷售量![]() 數據做了初步處理,得到如圖的散點圖及一些統計量的值.
數據做了初步處理,得到如圖的散點圖及一些統計量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根據散點圖判斷,![]() 可以作為年銷售量
可以作為年銷售量![]() (萬件)關于年營銷費用
(萬件)關于年營銷費用![]() (萬元)的回歸方程.
(萬元)的回歸方程.
①求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
⑦用所求的回歸方程估計該企業應投人多少年營銷費,才能使得該企業的年收益的預報值達到最大?(收益=銷售利潤營銷費用,取![]() )
)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() 其回歸直線
其回歸直線![]() 均斜率和截距的最小二乘估計分別為
均斜率和截距的最小二乘估計分別為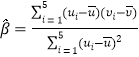 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某企業有職工5000人,其中男職工3500人,女職工1500人.該企業為了豐富職工的業余生活,決定新建職工活動中心,為此,該企業工會采用分層抽樣的方法,隨機抽取了300名職工每周的平均運動時間(單位:h),匯總得到頻率分布表(如表所示),并據此來估計該企業職工每周的運動時間:
平均運動時間 | 頻數 | 頻率 |
[0,2) | 15 | 0.05 |
[2,4) | m | 0.2 |
[4,6) | 45 | 0.15 |
[6,8) | 755 | 0.25 |
[8,10) | 90 | 0.3 |
[10,12) | p | n |
合計 | 300 | 1 |
(1)求抽取的女職工的人數;
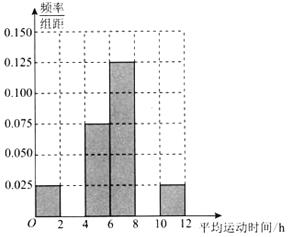
(2)①根據頻率分布表,求出m、n、p的值,完成如圖所示的頻率分布直方圖,并估計該企業職工每周的平均運動時間不低于4h的概率;
男職工 | 女職工 | 總計 | |
平均運動時間低于4h | |||
平均運動時間不低于4h | |||
總計 |
②若在樣本數據中,有60名女職工每周的平均運動時間不低于4h,請完成以下2×2列聯表,并判斷是否有95%以上的把握認為“該企業職工毎周的平均運動時間不低于4h與性別有關”.
附:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,過
,過![]() 點作
點作![]() 的垂線,交
的垂線,交![]() 的延長線于點
的延長線于點![]() ,
,![]() .連結
.連結![]() ,交
,交![]() 于點
于點![]() ,如圖1,將
,如圖1,將![]() 沿
沿![]() 折起,使得點
折起,使得點![]() 到達點
到達點![]() 的位置,如圖2.
的位置,如圖2.
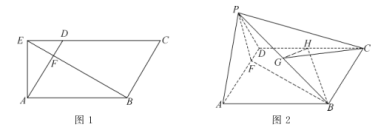
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,且平面
的中點,且平面![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 經過點
經過點![]() ,左、右焦點分別是
,左、右焦點分別是![]() ,
,![]() ,
,![]() 點在橢圓上,且滿足
點在橢圓上,且滿足![]() 的
的![]() 點只有兩個.
點只有兩個.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過![]() 且不垂直于坐標軸的直線
且不垂直于坐標軸的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,在
兩點,在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得
,使得![]() 的角平分線是
的角平分線是![]() 軸?若存在求出
軸?若存在求出![]() ,若不存在,說明理由.
,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,在圓
,在圓![]() :
:![]() 上任取一點
上任取一點![]() ,
,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() .(如圖).
.(如圖).

(1)求點![]() 的軌跡方程
的軌跡方程![]() ;
;
(2)若過點![]() 的動直線
的動直線![]() 與(1)中的軌跡
與(1)中的軌跡![]() 相交于
相交于![]() 、
、![]() 兩點.問:平面內是否存在異于點
兩點.問:平面內是否存在異于點![]() 的定點
的定點![]() ,使得
,使得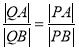 恒成立?試證明你的結論.
恒成立?試證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的焦距為
的焦距為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 為坐標原點).
為坐標原點).
(1)求橢圓![]() 的標準方程.
的標準方程.
(2)已知動直線![]() 與圓
與圓![]() :
:![]() 相切,且與橢圓
相切,且與橢圓![]() 交于
交于![]() ,
,![]() 兩點.是否存在實數
兩點.是否存在實數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
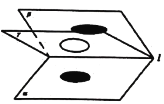
【題目】如圖,![]() ,
,![]() ,
,![]() 是由直線
是由直線![]() 引出的三個不重合的半平面,其中二面角
引出的三個不重合的半平面,其中二面角![]() 大小為60°,
大小為60°,![]() 在二面角
在二面角![]() 內繞直線
內繞直線![]() 旋轉,圓
旋轉,圓![]() 在
在![]() 內,且圓
內,且圓![]() 在
在![]() ,
,![]() 內的射影分別為橢圓
內的射影分別為橢圓![]() ,
,![]() .記橢圓
.記橢圓![]() ,
,![]() 的離心率分別為
的離心率分別為![]() ,
,![]() ,則
,則![]() 的取值范圍是( )
的取值范圍是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過兩點A(0,4),B(4,6),且圓心在直線x﹣2y﹣2=0上.
(1)求圓C的方程;
(2)若直線l過原點且被圓C截得的弦長為6,求直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com