
【題目】已知![]() (m,n為常數),在
(m,n為常數),在![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅰ)求![]() 的解析式并寫出定義域;
的解析式并寫出定義域;
(Ⅱ)若![]() ,使得對
,使得對![]() 上恒有
上恒有![]() 成立,求實數
成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若![]() 有兩個不同的零點
有兩個不同的零點![]() ,求證:
,求證:![]() .
.
【答案】(Ⅰ)![]() ,x∈(0,+∞);(Ⅱ)
,x∈(0,+∞);(Ⅱ)![]() ;(Ⅲ)詳見解析.
;(Ⅲ)詳見解析.
【解析】
(Ⅰ)利用導數的幾何意義意義求得m,n的值,根據對數函數的定義得到函數定義域;
(Ⅱ)f(x)在[![]() ,1]上的最小值為f(1)=1,只需t3﹣t2﹣2at+2≤1,即
,1]上的最小值為f(1)=1,只需t3﹣t2﹣2at+2≤1,即![]() 對任意的
對任意的![]() 上恒成立,構造函數m(t),利用導數求出m(t)的最大值,即可求得結論;
上恒成立,構造函數m(t),利用導數求出m(t)的最大值,即可求得結論;
(Ⅲ)不妨設x1>x2>0,得到g(x1)=g(x2)=0,根據相加和相減得到![]() ,再利用分析法,構造函數,求出函數單調性和函數的最小值,問題得以證明.
,再利用分析法,構造函數,求出函數單調性和函數的最小值,問題得以證明.
解:(Ⅰ)由f(x)=![]() +nlnx可得
+nlnx可得![]() ,
,
由條件可得![]() ,把x=-1代入x+y=2可得,y=1,
,把x=-1代入x+y=2可得,y=1,
∴![]() ,∴m=2,
,∴m=2,![]() ,∴
,∴![]() ,x∈(0,+∞),
,x∈(0,+∞),
(Ⅱ)由(Ⅰ)知f(x)在![]() 上單調遞減,∴f(x)在
上單調遞減,∴f(x)在![]() 上的最小值為f(1)=1,
上的最小值為f(1)=1,
故只需t3-t2-2at+2≤1,即![]() 對任意的
對任意的![]() 上恒成立,
上恒成立,
令![]() ,
,![]()
易求得m(t)在![]() 單調遞減,[1,2]上單調遞增,
單調遞減,[1,2]上單調遞增,
而![]() ,
,![]() ,∴2a≥m(t)max=g(2),∴
,∴2a≥m(t)max=g(2),∴![]() ,即a的取值范圍為
,即a的取值范圍為![]()
(Ⅲ)∵![]() ,不妨設x1>x2>0,
,不妨設x1>x2>0,
∴g(x1)=g(x2)=0,
∴![]() ,
,![]() ,相加可得
,相加可得![]() ,相減可得
,相減可得![]() ,
,
由兩式易得:![]() ;要證
;要證![]() ,即證明
,即證明![]() ,即證:
,即證:![]() ,需證明
,需證明![]() 成立,令
成立,令![]() ,則t>1,于是要證明
,則t>1,于是要證明![]() ,構造函數
,構造函數![]() ,∴
,∴![]() ,故(t)在(1,+∞)上是增函數,
,故(t)在(1,+∞)上是增函數,
∴(t)>(1)=0,∴![]() ,故原不等式成立.
,故原不等式成立.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】設集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求實數a的值;
(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市交管部門為了宣傳新交規舉辦交通知識問答活動,隨機對該市15~65歲的人群抽樣,回答問題統計結果如圖表所示.

組別 | 分組 | 回答正確的人數 | 回答正確的人數占本組的概率 |
第1組 | [15,25) | 5 | 0.5 |
第2組 | [25,35) |
| 0.9 |
第3組 | [35,45) | 27 |
|
第4組 | [45,55) |
| 0.36 |
第5組 | [55,65) | 3 |
|
(1)分別求出![]() 的值;
的值;
(2)從第2,3,4組回答正確的人中用分層抽樣方法抽取6人,則第2,3,4組每組應各抽取多少人?
(3)在(2)的前提下,決定在所抽取的6人中隨機抽取2人頒發幸運獎,求:所抽取的人中第2組至少有1人獲得幸運獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,點
,點![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.

(![]() )求橢圓
)求橢圓![]() 的方程.
的方程.
(![]() )若過點
)若過點![]() 且斜率不為
且斜率不為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,已知直線
兩點,已知直線![]() 與
與![]() 相交于點
相交于點![]() ,試判斷點
,試判斷點![]() 是否在定直線上?若是,請求出定直線的方程;若不是,請說明理由.
是否在定直線上?若是,請求出定直線的方程;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】到2020年,我國將全面建立起新的高考制度,新高考采用![]() 模式,其中語文、數學、英語三科為必考科目,滿分各150分,另外考生還要依據想考取的高校及專業的要求,結合自己的興趣、愛好等因素,在思想政治、歷史、地理、物理、化學、生物6門科目中自選3門(6選3)參加考試,滿分各100分.為了順利迎接新高考改革,某學校采用分層抽樣的方法從高一年級1000名(其中男生550名,女生450名)學生中抽取了
模式,其中語文、數學、英語三科為必考科目,滿分各150分,另外考生還要依據想考取的高校及專業的要求,結合自己的興趣、愛好等因素,在思想政治、歷史、地理、物理、化學、生物6門科目中自選3門(6選3)參加考試,滿分各100分.為了順利迎接新高考改革,某學校采用分層抽樣的方法從高一年級1000名(其中男生550名,女生450名)學生中抽取了![]() 名學生進行調查.
名學生進行調查.
(1)已知抽取的![]() 名學生中有女生45名,求
名學生中有女生45名,求![]() 的值及抽取的男生的人數.
的值及抽取的男生的人數.
(2)該校計劃在高一上學期開設選修中的“物理”和“地理”兩個科目,為了解學生對這兩個科目的選課情況,對在(1)的條件下抽取到的![]() 名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目,且只能選擇一個科目),得到如下
名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目,且只能選擇一個科目),得到如下![]() 列聯表.
列聯表.
選擇“物理” | 選擇“地理” | 總計 | |
男生 | 10 | ||
女生 | 25 | ||
總計 |
(i)請將列聯表補充完整,并判斷是否有![]() 以上的把握認為選擇科目與性別有關系.
以上的把握認為選擇科目與性別有關系.
(ii)在抽取的選擇“地理”的學生中按性別分層抽樣抽取6名,再從這6名學生中抽取2名,求這2名中至少有1名男生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2016年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組,得到的頻率分布表如表所示.
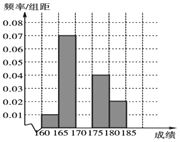
組號 | 分組 | 頻數 | 頻率 |
第1組 |
| 5 |
|
第2組 |
| n |
|
第3組 |
| 30 | p |
第4組 |
| 20 |
|
第5組 |
| 10 |
|
合計 | 100 |
|
(1)求頻率分布表中n,p的值,完善頻率分布直方圖并估計該組數據的中位數![]() 保留l位小數
保留l位小數![]() ;
;
(2)為了能選拔出最優秀的學生,高校決定在筆試成績高的第3、4、5組中用分層抽樣的方法抽取6名學生進入第二輪面試,學校決定從這6名學生中隨機抽取2名學生接受甲考官的面試,求第4組至少有1名學生被甲考官面試的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com