
【題目】已知![]() .
.
(1)當![]() 時,求不等式
時,求不等式![]() 的解集;
的解集;
(2)若![]() 時,不等式
時,不等式![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】
(1)將a=1代入f(x)中,去絕對值后分別解不等式即可;
(2)x∈(0,1)時,不等式f(x)<x+2恒成立等價于當x∈(0,1)時,|ax-1|<1恒成立,然后分a≤0和a>0討論即可.
解:(1)解法1:當![]() 時,不等式
時,不等式![]() 可化簡為
可化簡為![]() .
.
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
當![]() 時,
時,![]() ,
,![]() ,無解;
,無解;
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() ﹒
﹒
綜上,不等式![]() 的解集為
的解集為![]() .
.
解法2:當![]() 時,
時,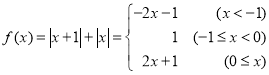
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
當![]() 時,
時,![]() ,無解;
,無解;
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() .
.
綜上,不等式![]() 的解集為
的解集為![]() .
.
(2)解法1:當![]() 時,不等式
時,不等式![]() 可化簡為
可化簡為![]() .
.
令![]() ,則
,則![]() 的圖像為過定點
的圖像為過定點![]() 斜率為a的一條直線,
斜率為a的一條直線,
數形結合可知,當![]() 時,
時,![]() 在
在![]() 上恒成立.
上恒成立.
所以,所求a的取值范圍為
解法2:當![]() 時,不等式
時,不等式![]() 可化簡為
可化簡為![]() .
.
由不等式的性質得![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
當![]() 時,
時,![]() ,不等式
,不等式![]() 不恒成立;
不恒成立;
為使不等式![]() 恒成立,則
恒成立,則![]() .
.
綜上,所求a的取值范圍為 .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() 為自然對數的底數. 設
為自然對數的底數. 設![]() 是
是![]() 的導函數.
的導函數.
(Ⅰ)若![]() 時,函數
時,函數![]() 在
在![]() 處的切線經過點
處的切線經過點![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函數![]() 在區間
在區間![]() 上的單調區間;
上的單調區間;
(Ⅲ)若![]() ,函數
,函數![]() 在區間
在區間![]() 內有零點,求
內有零點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年3月18日,國務院辦公廳發布了《生活垃圾分類制度實施方案》,我市環保部門組織了一次垃圾分類知識的網絡問卷調查,每位市民都可以通過電腦網絡或手機微信平臺參與,但僅有一次參加機會工作人員通過隨機抽樣,得到參與網絡問卷調查的100人的得分(滿分按100分計)數據,統計結果如下表.
組別 |
|
|
|
|
|
|
女 | 2 | 4 | 4 | 15 | 21 | 9 |
男 | 1 | 4 | 10 | 10 | 12 | 8 |
(1)環保部門規定:問卷得分不低于70分的市民被稱為“環保關注者”.請列出![]() 列聯表,并判斷能否在犯錯誤的概率不超過
列聯表,并判斷能否在犯錯誤的概率不超過![]() 的前提下,認為是否為“環保關注者”與性別有關?
的前提下,認為是否為“環保關注者”與性別有關?
(2)若問卷得分不低于80分的人稱為“環保達人”.現在從本次調查的“環保達人”中利用分層抽樣的方法隨機抽取5名市民參與環保知識問答,再從這5名市民中抽取2人參與座談會,求抽取的2名市民中,既有男“環保達人”又有女“環保達人”的概率.
附表及公式: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農科站技術員為了解某品種樹苗的生長情況,在該批樹苗中隨機抽取一個容量為100的樣本,測量樹苗高度(單位:cm).經統計,高度均在區間[20,50]內,將其按[20,25),[25,30),[30,35),[35,40),[40,45),[45,50]分成6組,制成如圖所示的頻率分布直方圖,其中高度不低于40cm的樹苗為優質樹苗.
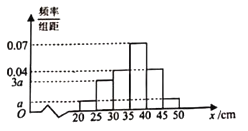
(1)已知所抽取的這100棵樹苗來自于甲、乙兩個地區,部分數據如下2×2列聯表所示,將列聯表補充完整,并根據列聯表判斷是否有99.9%的把握認為優質樹苗與地區有關?
(2)用樣本估計總體的方式,從這批樹苗中隨機抽取4棵,期中優質樹苗的棵數記為X,求X的分布列和數學期望.
甲地區 | 乙地區 | 合計 | |
優質樹苗 | 5 | ||
非優質樹苗 | 25 | ||
合計 |
附:K2=![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com