【題目】某種商品原來每件售價為25元，年銷售8萬件．
（1）據市場調查，若價格每提高1元，銷售量將相應減少2000件，要使銷售的總收入不低于原收入，該商品每件定價最多為多少元？
（2）為了擴大該商品的影響力，提高年銷售量，公司決定明年對該商品進行全面技術革新和營銷策略改革，并提高定價到
元，公司擬投入
萬元作為技改費用，投入50萬元作為固定宣傳費用，投入
作為浮動宣傳費用．試問：當該商品明年的銷售量
至少應達到多少萬件時，才可能使明年的銷售收入不低于原收入與總投入之和？并求出此時商品的每件定價．
【答案】（1）每件定價最多為
元；（2）當該商品明年的銷售量
至少達到
萬件時，才可能使明年的銷售收入不低于原收入與總收入之和，此時該商品的每件定價為
元．
【解析】
試題分析：（1）設每件定價為
元，依題意，得
，解不等式即可求解結論；（2）依題意
時，不等式
有解，等價于時，得到
有解，利用基本不等式，即可得到結論．
試題解析：（1）設每件定價為元，
依題意，有，
整理得
，解得
，
∴要使銷售的總收入不低于原收入，每件定價最多為40元．
（2）依題意，當時，不等式有解，
即
時，不等式有解．
∵
（當且僅當
時，等號成立），∴
．
∴當該商品明年的銷售量至少達到10.2萬件時，才可能使明年的銷售收入不低于原收入與總收入之和，此時該商品的每件定價為30元．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】圍建一個面積為360
的矩形場地，要求矩形場地的一面利用舊墻（利用舊墻需維修），其它三面圍墻要新建，在舊墻的對面的新墻上要留一個寬度為2m的進出口，如圖所示，已知舊墻的維修費用為45元/m,新墻的造價為180元/m,設利用的舊墻的長度為
（單位：
），修建此矩形場地圍墻的總費用為
（單位：元）
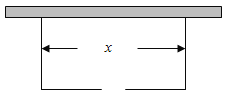
（1）將表示為的函數；
（2）試確定,使修建此矩形場地圍墻的總費用最小，并求出最小總費用。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了了解我校高2017級本部和大學城校區的學生是否愿意參加自主招生培訓的情況，對全年級2000名高三學生進行了問卷調查，統計結果如下表：
校區 | 愿意參加 | 不愿意參加 |
重慶一中本部校區 | 220 | 980 |
重慶一中大學城校區 | 80 | 720 |
（1）若從愿意參加自主招生培訓的同學中按分層抽樣的方法抽取15人，則大學城校區應抽取幾人；
（2）現對愿意參加自主招生的同學組織摸底考試，考試題共有5道題，每題20分，對于這5道題，考生“如花姐”完全會答的有3題，不完全會的有2道，不完全會的每道題她得分
的概率滿足：
，假設解答各題之間沒有影響，
①對于一道不完全會的題，求“如花姐”得分的均值
；
②試求“如花姐”在本次摸底考試中總得分的數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的奇數項是公差為
的等差數列，偶數項是公差為
的等差數列， 
是數列
的前
項和， 
（1）若
，求
；
（2）已知
，且對任意的
，有
恒成立，求證：數列
是等差數列；
（3）若
，且存在正整數
，使得
，求當
最大時，數列
的通項公式.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市隨機抽取一年（365天）內100天的空氣質量指數
的檢測數據，結果統計如下：
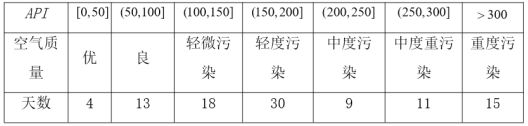
記某企業每天由空氣污染造成的經濟損失
（單位：元），空氣質量指數
為
．在區間
對企業沒有造成經濟損失；在區間
對企業造成經濟損失成直線模型（當
為150時造成的經濟損失為500元，當
為200時，造成的經濟損失為700元）；當
大于300時造成的經濟損失為2000元．
（1）試寫出
的表達式；
（2）試估計在本年內隨機抽取一天，該天經濟損失
大于200元且不超過600元的概率；
（3）若本次抽取的樣本數據有30天是在供暖季，其中有8天為重度污染，完成下面
列聯表，并判斷
能否有
的把握認為該市本年空氣重度污染與供暖有關？
附：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.82 |
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數f(x)和g(x)滿足：①在區間[a，b]上均有定義；②函數y＝f(x)－g(x)在區間[a，b]上至少有一個零點，則稱f(x)和g(x)在[a，b]上具有關系G．
（1）若f(x)＝lgx，g(x)＝3－x，試判斷f(x)和g(x)在[1，4]上是否具有關系G，并說明理由；
（2）若f(x)＝2|x－2|＋1和g(x)＝mx2在[1，4]上具有關系G，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）若關于
的方程
在區間
上有兩個不同的解
．
（ⅰ）求
的取值范圍；
（ⅱ）若
，求
的取值范圍；
（2）設函數
在區間
上的最大值和最小值分別為
，求
的表達式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
