
【題目】在如圖所示的幾何體中,四邊形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
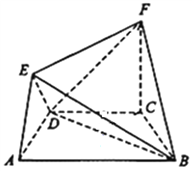
(1)求證: ![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)見解析;(2)直線![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
【解析】試題分析:(1)要證線面平行,先找線線平行,先證平面AED⊥平面ABCD,做過E作EG⊥AD于G,則EG⊥平面ABCD,∴FC∥EG,進而得到線面平行;(2)建系,求面的法向量和線的方向向量,根據向量夾角得到線面角,即可。
解析:
(Ⅰ)證明:∵四邊形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴BC=DC,∠ADC=∠BCD=120°,∴∠CDB=30°,
∴∠ADB=90°,即BD⊥AD.
又AE⊥BD, ![]() =A,∴BD⊥平面AED,
=A,∴BD⊥平面AED,
又BD![]() 平面ABCD,∴平面AED⊥平面ABCD.
平面ABCD,∴平面AED⊥平面ABCD.
如圖4,過E作EG⊥AD于G,則EG⊥平面ABCD,
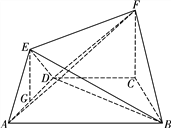
又FC⊥平面ABCD,∴FC∥EG.
又EG![]() 平面AED,FC
平面AED,FC![]() 平面AED,
平面AED,
∴FC∥平面AED.
(Ⅱ)解:如圖5,連接AC,由(Ⅰ)知AC⊥BC,
∵FC⊥平面ABCD,
∴CA,CB,CF兩兩垂直.
以C為原點,建立空間直角坐標系Cxyz.
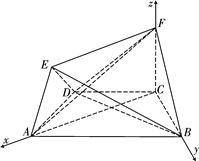
設BC![]() ,則AC
,則AC![]() ,AB
,AB![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,
, ![]() .
.
設平面BDF的法向量為![]() ,
,
則![]() 即
即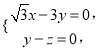
令![]() ,則
,則![]() ,
, ![]() ,則
,則![]() .
.
設直線AF與平面BDF所成角為![]() ,則
,則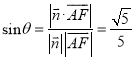 ,
,
故直線AF與平面BDF所成角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某地區(qū)2007年至2013年農村居民家庭純收入y(單位:千元)的數據如下表:

(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)利用(Ⅰ)中的回歸方程,分析2007年至2013年該地區(qū)農村居民家庭人均純收入的變化情況,并預測該地區(qū)2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
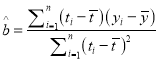 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
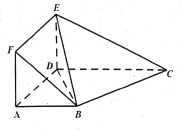
【題目】如圖,在幾何體![]() 中,四邊形
中,四邊形![]() 為矩形,四邊形
為矩形,四邊形![]() 為梯形,
為梯形, ![]() ,平面
,平面![]() 與平面
與平面![]() 垂直,且
垂直,且![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() ,且平面
,且平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】無窮數列![]() 滿足:
滿足: ![]() 為正整數,且對任意正整數
為正整數,且對任意正整數![]() ,
, ![]() 為前
為前![]() 項
項![]() ,
, ![]() ,
, ![]() ,
, ![]() 中等于
中等于![]() 的項的個數.
的項的個數.
(Ⅰ)若![]() ,請寫出數列
,請寫出數列![]() 的前7項;
的前7項;
(Ⅱ)求證:對于任意正整數![]() ,必存在
,必存在![]() ,使得
,使得![]() ;
;
(Ⅲ)求證:“![]() ”是“存在
”是“存在![]() ,當
,當![]() 時,恒有
時,恒有![]()
![]() 成立”的充要條件。
成立”的充要條件。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·太原三模)已知等比數列{an}的各項均為不等于1的正數,數列{bn}滿足bn=lgan,b3=18,b6=12,則數列{bn}的前n項和的最大值為( )
A. 126 B. 130 C. 132 D. 134
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點M(﹣1,0),N(1,0),曲線E上任意一點到點M的距離均是到點N的距離的![]() 倍.
倍.
(1)求曲線E的方程;
(2)已知m≠0,設直線![]() :x﹣my﹣1=0交曲線E于A,C兩點,直線
:x﹣my﹣1=0交曲線E于A,C兩點,直線![]() :mx+y﹣m=0交曲線E于B,D兩點,若CD的斜率為﹣1時,求直線CD的方程.
:mx+y﹣m=0交曲線E于B,D兩點,若CD的斜率為﹣1時,求直線CD的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
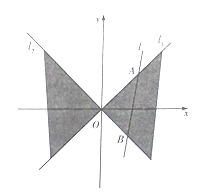
【題目】【2018河南安陽市高三一模】如下圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與直線
與直線![]() 之間的陰影部分即為
之間的陰影部分即為![]() ,區(qū)域
,區(qū)域![]() 中動點
中動點![]() 到
到![]() 的距離之積為1.
的距離之積為1.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)動直線![]() 穿過區(qū)域
穿過區(qū)域![]() ,分別交直線
,分別交直線![]() 于
于![]() 兩點,若直線
兩點,若直線![]() 與軌跡
與軌跡![]() 有且只有一個公共點,求證:
有且只有一個公共點,求證: ![]() 的面積恒為定值.
的面積恒為定值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com