【題目】已知直線l的極坐標方程為ρsin（θ+ 
）= 
．
（1）在極坐標系下寫出θ=0和θ= 
時該直線上的兩點的極坐標，并畫出該直線；
（2）已知Q是曲線ρ=1上的任意一點，求點Q到直線l的最短距離及此時Q的極坐標．
【答案】
（1）解：直線l經過A（2，0）， 
兩點，
在極坐標系下，直線如圖所示：
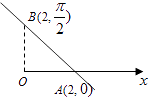
（2）解：曲線ρ=1化為直角坐標方程得x2+y2=1，該曲線為單位圓，
將直線l的極坐標方程 
化為直角坐標方程得x+y﹣2=0
要求圓上任意一點到直線l的最短距離，只要求圓心O（0，0）到直線l的距離即可．
由點到直線的距離公式得： 
，
所以點Q到直線l的最短距離為 
，
此時，點Q的極坐標為 
．
【解析】（1）將θ=0和θ= 
分別代入直線l的極坐標方程，求出ρ，從而得出兩點的極坐標，畫出直線；（2）分別求出直線l和曲線ρ=1的直角坐標方程，要求圓上任意一點到直線l的最短距離，只要求圓心O（0，0）到直線l的距離即可．
科目：高中數學 來源： 題型：
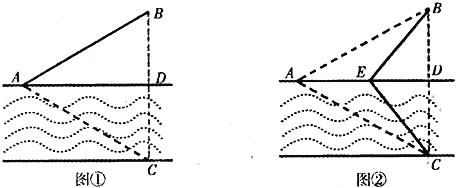
【題目】如圖①，一條寬為1km的兩平行河岸有村莊A和供電站C，村莊B與A、C的直線距離都是2km，BC與河岸垂直，垂足為D．現要修建電纜，從供電站C向村莊A、B供電．修建地下電纜、水下電纜的費用分別是2萬元/km、4萬元/km．
（1）已知村莊A與B原來鋪設有舊電纜，但舊電纜需要改造，改造費用是0.5萬元/km．現決定利用此段舊電纜修建供電線路，并要求水下電纜長度最短，試求該方案總施工費用的最小值；
（2）如圖②，點E在線段AD上，且鋪設電纜的線路為CE、EA、EB．若∠DCE＝θ(0≤θ≤
)，試用θ表示出總施工費用y (萬元)的解析式，并求y的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
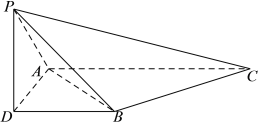
【題目】如圖，三棱錐
，側棱
，底面三角形
為正三角形，邊長為
，頂點
在平面
上的射影為
，有
，且
.
（Ⅰ）求證： 
平面
；
（Ⅱ）求二面角
的余弦值；
（Ⅲ）線段
上是否存在點
使得
⊥平面
，如果存在，求
的值；如果不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學舉行了一次“環保知識競賽”活動．為了了解本次競賽學生成績情況，從中抽取了部分學生的分數（得分取正整數，滿分為100分）作為樣本（樣本容量為n）進行統計．按照
，
，
，
，
的分組作出頻率分布直方圖，并作出樣本分數的莖葉圖（圖中僅列出了得分在，的數據）．
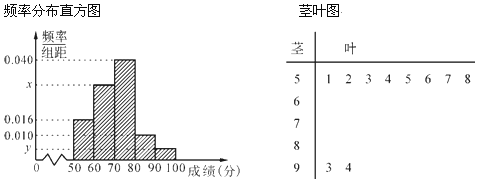
（1）求樣本容量n和頻率分布直方圖中x、y的值;
（2）在選取的樣本中，從競賽成績是80分以上（含80分）的同學中隨機抽取2名同學到市政廣場參加環保知識宣傳的志愿者活動，求所抽取的2名同學來自不同組的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ex（其中e為自然對數的底數），g（x）=
x+m（m，n∈R）．
（1）若T（x）=f（x）g（x），m=1﹣
，求T（x）在[0，1]上的最大值；
（2）若m=﹣
，n∈N*，求使f（x）的圖象恒在g（x）圖象上方的最大正整數n．[注意：7＜e2＜
]．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
