
���}Ŀ����D��ʾ��O������߅��ABCDEF�����ģ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
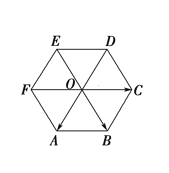
��1���c![]() ���L(zh��ng)����ȡ������෴����������Щ��
���L(zh��ng)����ȡ������෴����������Щ��
��2���c![]() ����������������
����������������
��3��Ո(q��ng)һһ�г��c![]() ��
��![]() ��
��![]() .��ȵ�������
.��ȵ�������
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() .��2��
.��2��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
��3���c![]() ��ȵ�������
��ȵ�������![]() ��
��![]() ��
��![]() ���c
���c![]() ��ȵ�������
��ȵ�������![]() ��
��![]() ��
��![]() ���c
���c![]() ��ȵ�������
��ȵ�������![]() ��
��![]() ��
��![]() .
.
��������
��1������(j��)����߅�ε����|(zh��)���D���и������L(zh��ng)�ȶ���ȣ�ֻҪ�����෴����.
��2������(j��)���������������.
��3������(j��)��ȵ������Ķ��x���.
��1����?y��n)�����߅���и������L(zh��ng)�ȶ���ȣ��ҷ����෴���У�![]() ��
��![]() ��
��![]() ��
��![]() .��2���ɹ������������ã�
.��2���ɹ������������ã�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .�c
.�c![]() ����.
����.
��3������������Ķ��x�ã��c![]() ��ȵ�������
��ȵ�������![]() ��
��![]() ��
��![]() ���c
���c![]() ��ȵ�������
��ȵ�������![]() ��
��![]() ��
��![]() ���c
���c![]() ��ȵ�������
��ȵ�������![]() ��
��![]() ��
��![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����̞�![]() ���������o�������Ă�(g��)�Y(ji��)Փ��
���������o�������Ă�(g��)�Y(ji��)Փ��
�� �P(gu��n)��![]() �S��(du��)�Q��
�S��(du��)�Q��
�� �P(gu��n)������(bi��o)ԭ�c(di��n)��(du��)�Q��
�� �P(gu��n)��![]() �S��(du��)�Q��
�S��(du��)�Q��
�� ![]() ��
��![]() ��
��
���ϽY(ji��)Փ���_�Ă�(g��)��(sh��)�ǣ� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪0<��<![]() <��<��,cos
<��<��,cos![]() ,sin(��+��)=
,sin(��+��)=![]() .
.
(1)��sin 2����ֵ;(2)��cos![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�AE��һ��(g��)��c(di��n)��![]() �����c(di��n)��x�S�ϣ����E�A���ҽ��c(di��n)��ֱ��
�����c(di��n)��x�S�ϣ����E�A���ҽ��c(di��n)��ֱ��![]() �ľ��x��3��
�ľ��x��3��
![]() ��E�AE�ķ��̣�
��E�AE�ķ��̣�
![]() �O(sh��)�^(gu��)�c(di��n)A��ֱ��l�cԓ�E�A������һ�c(di��n)B����(d��ng)��AB���L(zh��ng)�����r(sh��)����ֱ��l�ķ��̣�
�O(sh��)�^(gu��)�c(di��n)A��ֱ��l�cԓ�E�A������һ�c(di��n)B����(d��ng)��AB���L(zh��ng)�����r(sh��)����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
![]() .
.
��������(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ��
��![]() ̎���о����̣�
̎���о����̣�
��������(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
������������(sh��)![]() �Ѓɂ�(g��)�Oֵ�c(di��n)
�Ѓɂ�(g��)�Oֵ�c(di��n)![]() ������ʽ
������ʽ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)![]() �ǒ��タ
�ǒ��タ![]() �Ľ��c(di��n)�����c(di��n)
�Ľ��c(di��n)�����c(di��n)![]() �ڒ��タ
�ڒ��タ![]() �ϣ���
�ϣ���![]()
![]() ���タ
���タ![]() �ķ��̣�
�ķ��̣�
![]() ��(d��ng)ֱ��
��(d��ng)ֱ��![]() �c���タ
�c���タ![]() �ཻ��
�ཻ��![]() ���c(di��n)����(w��n)����
���c(di��n)����(w��n)����![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() ����
����![]() ��ʹ������
��ʹ������![]() �c����
�c����![]() ����
����![]() ����
����![]() ������(bi��o)ԭ�c(di��n)
������(bi��o)ԭ�c(di��n)![]() �������ڣ�����c(di��n)
�������ڣ�����c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪ż����(sh��)![]() �M��
�M��![]() ��
��![]() ����(d��ng)
����(d��ng)![]() �r(sh��),
�r(sh��),![]() ���P(gu��n)��
���P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ��
��![]() ������ֻ��200��(g��)����(sh��)�⣬�t��(sh��)��(sh��)
������ֻ��200��(g��)����(sh��)�⣬�t��(sh��)��(sh��)![]() ��ȡֵ�����飨 ��
��ȡֵ�����飨 ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪����ֱ��������![]() ��б߅
��б߅![]() ����ֱ�����̞�
����ֱ�����̞�![]() ������
������![]() �c(di��n)��
�c(di��n)��![]() �c(di��n)�Ϸ���ֱ����c(di��n)
�c(di��n)�Ϸ���ֱ����c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��
��

��1����![]() ߅�ϵĸ߾�
߅�ϵĸ߾�![]() ����ֱ���ķ��̣�
����ֱ���ķ��̣�
��2�������ֱ��������![]() ����ӈA�Ę�(bi��o)��(zh��n)���̣�
����ӈA�Ę�(bi��o)��(zh��n)���̣�
��3���քe���ֱ��߅![]() ��
��![]() ����ֱ���ķ��̣�
����ֱ���ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���P(gu��n)�ڿ��gֱ������(bi��o)ϵ![]() �е�һ�c(di��n)
�е�һ�c(di��n)![]() ���������f(shu��)����
���������f(shu��)����
���c(di��n)![]() ������(bi��o)ԭ�c(di��n)�ľ��x��
������(bi��o)ԭ�c(di��n)�ľ��x��![]() ��
��
��![]() �����c(di��n)����(bi��o)��
�����c(di��n)����(bi��o)��![]() ��
��
���c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q���c(di��n)������(bi��o)��
�S��(du��)�Q���c(di��n)������(bi��o)��![]() ��
��
���c(di��n)![]() �P(gu��n)������(bi��o)ԭ�c(di��n)��(du��)�Q���c(di��n)������(bi��o)��
�P(gu��n)������(bi��o)ԭ�c(di��n)��(du��)�Q���c(di��n)������(bi��o)��![]() ��
��
���c(di��n)![]() �P(gu��n)������(bi��o)ƽ��
�P(gu��n)������(bi��o)ƽ��![]() ��(du��)�Q���c(di��n)������(bi��o)��
��(du��)�Q���c(di��n)������(bi��o)��![]() .
.
�������_��(g��)��(sh��)��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com