
【題目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)當x∈[0, ![]() ]時,求|
]時,求| ![]() +
+ ![]() |的取值范圍;
|的取值范圍;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求當k為何值時,g(x)的最小值為﹣
,求當k為何值時,g(x)的最小值為﹣ ![]() .
.
【答案】
(1)解: ![]() =(sinx﹣2cosx,sinx),
=(sinx﹣2cosx,sinx),
| ![]() |2=(sinx﹣2cosx,sinx)2
|2=(sinx﹣2cosx,sinx)2
=2sin2x﹣4sinxcosx+4cos2x
=2cos2x﹣4sinxcosx+2
=cos2x﹣2sin2x+3
= ![]() cos(2x+φ)+3,其中,tanφ=2,
cos(2x+φ)+3,其中,tanφ=2,
又∵x∈[0, ![]() ],
],
∴ ![]() ,
,
∴ ![]() 在
在 ![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴| ![]() cos(2x+φ)|2∈[1,4],
cos(2x+φ)|2∈[1,4],
∴| ![]() +
+ ![]() |∈[1,2].
|∈[1,2].
(2)解: ![]() =(2sinx,cosx+k),
=(2sinx,cosx+k),
g(x)=( ![]() )
) ![]()
=﹣4sinxcosx+(cosx+k)(sinx﹣k)
=﹣3sinxcosx+k(sinx﹣cosx)﹣k2
令t=sinx﹣cosx= ![]() sin(x﹣
sin(x﹣ ![]() ),
),
則t∈[﹣ ![]() ,
, ![]() ],且t2=sin2x+cos2x﹣2sinxcosx=1﹣2sinxcosx,
],且t2=sin2x+cos2x﹣2sinxcosx=1﹣2sinxcosx,
所以 ![]() .
.
所以g(x)可化為 ![]() ,
,
對稱軸 ![]() .
.
① 當 ![]() ,即
,即 ![]() 時,
時, ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
所以 ![]() .
.
因為 ![]() ,
,
所以此時無解.
②當 ![]() ,即
,即 ![]() 時,
時, ![]() .
.
由﹣ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,得k=0∈[﹣3
,得k=0∈[﹣3 ![]() ,3
,3 ![]() ].
].
③當﹣ ![]()
![]() ,即k<﹣3
,即k<﹣3 ![]() 時,
時,
g(x)min=h( ![]() )=﹣k2+
)=﹣k2+ ![]() k+
k+ ![]() ,
,
由﹣k2+ ![]() k+
k+ ![]() =﹣
=﹣ ![]() ,得k2﹣
,得k2﹣ ![]() k﹣3=0,
k﹣3=0,
所以k= ![]() .
.
因為k ![]() ,所以此時無解.
,所以此時無解.
綜上所述,當k=0時,g(x)的最小值為﹣ ![]()
【解析】(1)由已知利用平面向量的坐標運算可得 ![]() =(sinx﹣2cosx,sinx),利用三角函數(shù)恒等變換的應(yīng)用可得|
=(sinx﹣2cosx,sinx),利用三角函數(shù)恒等變換的應(yīng)用可得| ![]() |2=
|2= ![]() cos(2x+φ)+3,其中,tanφ=2,又x∈[0,
cos(2x+φ)+3,其中,tanφ=2,又x∈[0, ![]() ],可求
],可求 ![]() ,利用余弦函數(shù)的單調(diào)性即可得解|
,利用余弦函數(shù)的單調(diào)性即可得解| ![]() |的取值范圍;(2)利用平面向量數(shù)量積的運算可得g(x)=﹣3sinxcosx+k(sinx﹣cosx)﹣k2 , 令t=sinx﹣cosx=
|的取值范圍;(2)利用平面向量數(shù)量積的運算可得g(x)=﹣3sinxcosx+k(sinx﹣cosx)﹣k2 , 令t=sinx﹣cosx= ![]() sin(x﹣
sin(x﹣ ![]() ),則g(x)可化為
),則g(x)可化為 ![]() ,對稱軸
,對稱軸 ![]() .利用二次函數(shù)的圖象和性質(zhì)分類討論即可得解.
.利用二次函數(shù)的圖象和性質(zhì)分類討論即可得解.


 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業(yè)江西人民出版社系列答案
波波熊暑假作業(yè)江西人民出版社系列答案 學而優(yōu)暑期銜接南京大學出版社系列答案
學而優(yōu)暑期銜接南京大學出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知實數(shù)λ>0,設(shè)函數(shù)f(x)=eλx﹣x.
(Ⅰ)當λ=1時,求函數(shù)f(x)的極值;
(Ⅱ)若對任意x∈(0,+∞),不等式f(x)≥0恒成立,求λ的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數(shù).
上的奇函數(shù).
(1)當![]() 時,
時, ![]() ,若當
,若當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)若![]() 的圖像關(guān)于
的圖像關(guān)于![]() 對稱,且
對稱,且![]() 時,
時, ![]() ,求當
,求當![]() 時,
時, ![]() 的解析式;
的解析式;
(3)當![]() 時,
時, ![]() .若對任意的
.若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知任意角θ以x軸非負半軸為始邊,若終邊經(jīng)過點P(x0 , y0),且|OP|=r(r>0),定義sicosθ= ![]() ,稱“sicosθ”為“正余弦函數(shù)”.對于正余弦函數(shù)y=sicosx,有同學得到如下結(jié)論: ①該函數(shù)是偶函數(shù);
,稱“sicosθ”為“正余弦函數(shù)”.對于正余弦函數(shù)y=sicosx,有同學得到如下結(jié)論: ①該函數(shù)是偶函數(shù);
②該函數(shù)的一個對稱中心是( ![]() ,0);
,0);
③該函數(shù)的單調(diào)遞減區(qū)間是[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
④該函數(shù)的圖象與直線y= ![]() 沒有公共點;
沒有公共點;
以上結(jié)論中,所有正確的序號是 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知常數(shù)![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() ,
, ![]() ;
;
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)若![]() ,且
,且![]() 是單調(diào)遞增數(shù)列,求實數(shù)
是單調(diào)遞增數(shù)列,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,
, ![]() ,對于任意給定的正整數(shù)
,對于任意給定的正整數(shù)![]() ,是否存在正整數(shù)
,是否存在正整數(shù)![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要寫出一組即可);若不存在,請說明理由;
的值(只要寫出一組即可);若不存在,請說明理由;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)f(x)=aln(x2+1)+bx,g(x)=bx2+2ax+b,(a>0,b>0).已知方程g(x)=0有兩個不同的非零實根x1 , x2 .
(1)求證:x1+x2<﹣2;
(2)若實數(shù)λ滿足等式f(x1)+f(x2)+3a﹣λb=0,求λ的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知F1 , F2為橢圓 ![]() 的左、右焦點,F(xiàn)2在以
的左、右焦點,F(xiàn)2在以 ![]() 為圓心,1為半徑的圓C2上,且|QF1|+|QF2|=2a.
為圓心,1為半徑的圓C2上,且|QF1|+|QF2|=2a.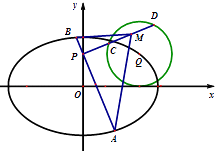
(1)求橢圓C1的方程;
(2)過點P(0,1)的直線l1交橢圓C1于A,B兩點,過P與l1垂直的直線l2交圓C2于C,D兩點,M為線段CD中點,求△MAB面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,側(cè)棱PD⊥底面ABCD,PD=DC,E是PC的中點,作EF⊥PB交PB于點F.
(1)證明PA∥平面EDB;
(2)證明PB⊥平面EFD;
(3)求二面角C﹣PB﹣D的大小.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com