
設函數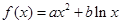 ,其中
,其中 .證明:當
.證明:當 時,函數
時,函數 沒有極值點;當
沒有極值點;當 時,函數
時,函數 有且只有一個極值點,并求出極值.
有且只有一個極值點,并求出極值.
當 時,函數
時,函數 沒有極值點;
沒有極值點;
當 時,
時,
若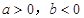 時,函數
時,函數 有且只有一個極小值點,極小值為
有且只有一個極小值點,極小值為 .
.
若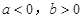 時,函數
時,函數 有且只有一個極大值點,極大值為
有且只有一個極大值點,極大值為 .
.
解析試題分析:證明:因為 ,所以
,所以 的定義域為
的定義域為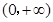 .
.
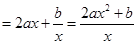 .
.
當 時,如果
時,如果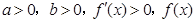 在
在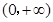 上單調遞增;
上單調遞增;
如果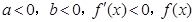 在
在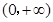 上單調遞減.
上單調遞減.
所以當 ,函數
,函數 沒有極值點.
沒有極值點.
當 時,
時,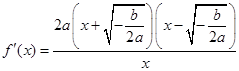
令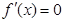 ,得
,得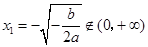 (舍去),
(舍去),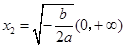 ,
,
當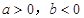 時,
時,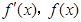 隨
隨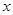 的變化情況如下表:
的變化情況如下表:
從上表可看出,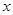
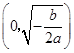
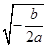
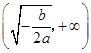

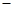
0 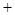

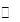
極小值 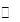
函數 有且只有一個極小值點,極小值為
有且只有一個極小值點,極小值為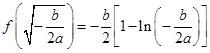 .
.
當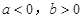 時,
時,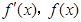 隨
隨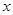 的變化情況如下表:
的變化情況如下表: