
【題目】已知函數![]() ,
,![]() .
.
(1)判斷![]() 的單調性,并證明之;
的單調性,并證明之;
(2)若存在實數![]() ,
,![]()
![]() ,使得函數
,使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]()
【解析】
(1)求出![]() 的定義域,判斷
的定義域,判斷![]() 的單調性,再利用單調性的定義證明即可.
的單調性,再利用單調性的定義證明即可.
(2)由(1)知,![]() 為偶函數,進而對
為偶函數,進而對![]() ,
,![]() 討論即可.
討論即可.
(1)由![]() ,得
,得![]() ,所以
,所以![]() 的定義域為
的定義域為![]() ,
,
![]() 在區間
在區間![]() 上為增函數,在區間
上為增函數,在區間![]() 上為減函數,
上為減函數,
證明如下:
任取![]() ,則
,則![]()
 ∵
∵![]() ,
,
∴![]() ,即
,即![]()
故![]() ,所以
,所以![]() 在區間
在區間![]() 上為減函數,
上為減函數,
同理可證,![]() 在區間
在區間![]() 上為增函數.
上為增函數.
綜上所述:![]() 在區間
在區間![]() 上為增函數,在區間
上為增函數,在區間![]() 上為減函數.
上為減函數.
(2)由(1)知![]() 為偶函數,且在區間
為偶函數,且在區間![]() 上為增函數,
上為增函數,
若存在![]() ,使得函數
,使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,即
,即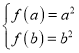 ,
,
則方程![]() ,即
,即![]() 在區間
在區間![]() 上有兩個不同的根,
上有兩個不同的根,
設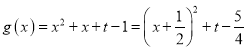 ,必有
,必有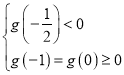 ,解得
,解得![]() ,
,
因![]() 為偶函數,則在區間
為偶函數,則在區間![]() 上存在實數
上存在實數![]() ,
,![]()
![]() ,使得函數
,使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,則有
,則有![]() ,
,
若存在![]() ,使得函數
,使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,
,
則有![]() ,
,![]() 或
或![]() ,
,
所以![]() ,則
,則![]() ,
,
若![]() 或
或![]() ,則
,則![]() 或
或![]() ,
,
即方程![]() 有兩個根
有兩個根![]() ,
,![]() ,其中
,其中![]() ,
,
因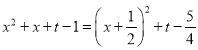 ,其對稱軸為
,其對稱軸為![]() ,故不存在實數
,故不存在實數![]() ,
,![]() 滿足題意,
滿足題意,
綜上所述:實數![]() 的取值范圍為
的取值范圍為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在Rt△ABC中,∠B=90°,BC=6,AB=8,點M為△ABC內切圓的圓心,過點M作動直線l與線段AB,AC都相交,將△ABC沿動直線l翻折,使翻折后的點A在平面BCM上的射影P落在直線BC上,點A在直線l上的射影為Q,則![]() 的最小值為_____.
的最小值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面![]() ,
,![]() 是兩個相交平面,其中
是兩個相交平面,其中![]() ,則
,則
A.平面![]() 內一定能找到與
內一定能找到與![]() 平行的直線
平行的直線
B.平面![]() 內一定能找到與
內一定能找到與![]() 垂直的直線
垂直的直線
C.若平面![]() 內有一條直線與
內有一條直線與![]() 平行,則該直線與平面
平行,則該直線與平面![]() 平行
平行
D.若平面![]() 內有無數條直線與
內有無數條直線與![]() 垂直,則平面
垂直,則平面![]() 與平面
與平面![]() 垂直
垂直
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中美貿易爭端一直不斷,2003年至2005年末,由美國單方面挑起的一系列貿易摩擦給中美貿易關系蒙上了濃重的陰影,貿易大戰似乎一觸即發,中美兩國進入了前所未有的貿易摩擦期.2018年,特朗普政府不顧中方勸阻,執意發動貿易戰,掀起了又一輪的中美貿易爭端.我國某種出口商品定價為每件60美元,美國不加收關稅時每年大約出口80萬件,中美經貿摩擦后,美國政府執意要加收進口關稅,每進口100美元商品要征稅P美元,因此每年出口量將減少![]() 萬件.
萬件.
(1)如果美國政府計劃每年對該商品加征的關稅金額不少于128萬美元,那么稅率應怎樣確定?
(2)在美國政府計劃每年對該商品加征關稅金額不少于128萬美元的前提下,如何確定稅率,才會使得我國生產該商品的廠家稅后獲取最大的出口額.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com