
【題目】有一組數據:1,1,4,5,5,5,則這組數據的眾數和中位數分別是( )
A.5和4
B.5和4.5
C.5和5
D.1和5
科目:高中數學 來源: 題型:
【題目】設向量 ![]() =(sin
=(sin ![]() x,cos
x,cos ![]() x),
x), ![]() =(sin
=(sin ![]() x,
x, ![]() sin
sin ![]() x),x∈R,函數f(x)=
x),x∈R,函數f(x)= ![]() ,求:
,求:
(1)f(x)的最小正周期;
(2)f(x)在區間[0,1]上的最大值和最小值,以及取得最大值和最小值時x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
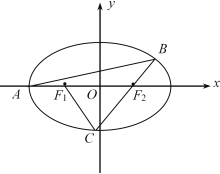
【題目】如圖,已知橢圓![]() 的左頂點
的左頂點![]() ,且點
,且點![]() 在橢圓上,
在橢圓上, ![]() 、
、![]() 分別是橢圓的左、右焦點。過點
分別是橢圓的左、右焦點。過點![]() 作斜率為
作斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于另一點
于另一點![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于點
于點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為等腰三角形,求點
為等腰三角形,求點![]() 的坐標;
的坐標;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學校本課程開設了A,B,C,D共4門選修課,每個學生必須且只能選修1門選修課,現有該校的甲、乙、丙3名學生.
(1)求這3名學生選修課所有選法的總數;
(2)求恰有2門選修課沒有被這3名學生選擇的概率;
(3)求A選修課被這3名學生選擇的人數ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐A﹣BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分別在線段AB,AC上,AP=3PB,AQ=2QC,M是BD的中點. 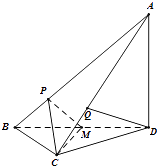
(Ⅰ)證明:DQ∥平面CPM;
(Ⅱ)若二面角C﹣AB﹣D的大小為 ![]() ,求∠BDC的正切值.
,求∠BDC的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國式過馬路”是網友對部分中國人集體闖紅燈現象的一種調侃,即“湊夠一撮人就可以走了,和紅綠燈無關.”出現這種現象是大家受法不責眾的“從眾”心理影響,從而不顧及交通安全.某校對全校學生過馬路方式進行調查,在所有參與調查的人中,“跟從別人闖紅燈”“從不闖紅燈”“帶頭闖紅燈”人數如表所示:
跟從別人闖紅燈 | 從不闖紅燈 | 帶頭闖紅燈 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(1)在所有參與調查的人中,用分層抽樣的方法抽取n人,已知“跟從別人闖紅燈”的人中抽取45人,求n的值;
(2)在“帶頭闖紅燈”的人中,將男生的200人編號為1,2,…,200;將女生的300人編號為201,202,…,500,用系統抽樣的方法抽取4人參加“文明交通”宣傳活動,若抽取的第一個人的編號為100,把抽取的4人看成一個總體,從這4人中任選取2人,求這兩人均是女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinx﹣cosx+x+1,x∈[0,2π]
(1)求函數f(x)的單調遞減區間;
(2)求函數f(x)的極小值和最大值,并寫明取到極小值和最大值時分別對應x的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com