
【題目】如圖,在三棱錐A﹣BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分別在線段AB,AC上,AP=3PB,AQ=2QC,M是BD的中點. 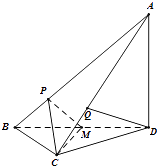
(Ⅰ)證明:DQ∥平面CPM;
(Ⅱ)若二面角C﹣AB﹣D的大小為 ![]() ,求∠BDC的正切值.
,求∠BDC的正切值.
【答案】證明:(Ⅰ)取AB的中點E,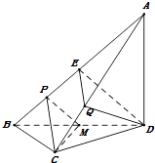
則 ![]() ,所以EQ∥PC.
,所以EQ∥PC.
又EQ平面CPM,所以EQ∥平面CPM.
又PM是△BDE的中位線,所以DE∥PM,
從而DE∥平面CPM.
所以平面DEQ∥平面CPM,
故DQ∥平面CPM.
解:(Ⅱ)解法1:由AD⊥平面BCD知,AD⊥CM
由BC=CD,BM=MD,知BD⊥CM,
故CM⊥平面ABD.
由(Ⅰ)知DE∥PM,而DE⊥AB,故PM⊥AB.
所以∠CPM是二面角C﹣AB﹣D的平面角,
即 ![]() .
.
設PM=a,則 ![]() ,
, ![]() ,
,
在Rt△CMD中, ![]() .
.
所以∠BDC的正切值為 ![]() .
.
解法2:以M為坐標原點,MC,MD,ME所在的直線分別為x軸,y軸,z軸,
建立如圖所示的空間直角坐標系.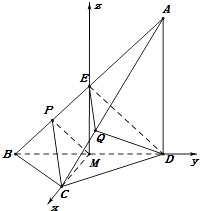
設MC=a,MD=b,則C(a,0,0),B(0,﹣b,0),A(0,b,2b)
則 ![]() ,
, ![]()
設 ![]() 平面ABC的一個法向量,
平面ABC的一個法向量,
則  即
即 ![]() 取
取 ![]()
平面ABD的一個法向量為 ![]() ,
,
所以 ![]() ,所以
,所以 ![]()
在Rt△CMD中, ![]()
所以∠BDC的正切值為 ![]() .
.
【解析】(Ⅰ)取AB的中點E,則EQ∥PC,從而EQ∥平面CPM,由中位線定理得DE∥PM,從而DE∥平面CPM,進而平面DEQ∥平面CPM,由此能證明DQ∥平面CPM.(Ⅱ)法1:推導出AD⊥CM,BD⊥CM,從而CM⊥平面ABD,進而得到∠CPM是二面角C﹣AB﹣D的平面角,由此能求出∠BDC的正切值.法2:以M為坐標原點,MC,MD,ME所在的直線分別為x軸,y軸,z軸,建立空間直角坐標系,利用向量法能求出∠BDC的正切值.
【考點精析】本題主要考查了直線與平面平行的判定的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行才能正確解答此題.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】下列四個命題中,正確的有( ) ①兩個變量間的相關系數r越小,說明兩變量間的線性相關程度越低;
②命題“x∈R,使得x2+x+1<0”的否定是:“對x∈R,均有x2+x+1>0”;
③命題“p∧q為真”是命題“p∨q為真”的必要不充分條件;
④若函數f(x)=x3+3ax2+bx+a2在x=﹣1有極值0,則a=2,b=9或a=1,b=3.
A.0 個
B.1 個
C.2 個
D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分圖象如圖所示
)的部分圖象如圖所示 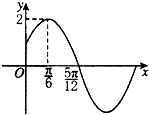
(1)求函數f(x)的解析式;
(2)分析該函數是如何通過y=sinx變換得來的?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,左右焦點分別為
,左右焦點分別為![]() 是橢圓在第一象限上的一個動點,圓
是橢圓在第一象限上的一個動點,圓![]() 與
與![]() 的延長線,
的延長線, ![]() 的延長線以及線段
的延長線以及線段![]() 都相切,
都相切, ![]() 為一個切點.
為一個切點.
(1)求橢圓方程;
(2)設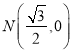 ,過
,過![]() 且不垂直于坐標軸的動點直線
且不垂直于坐標軸的動點直線![]() 交橢圓于
交橢圓于![]() 兩點,若以
兩點,若以![]() 為鄰邊的平行四邊形是菱形,求直線
為鄰邊的平行四邊形是菱形,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 某中學的環(huán)保社團參照國家環(huán)境標準制定了該校所在區(qū)域空氣質量指數與空氣質量等級對應關系如下表(假設該區(qū)域空氣質量指數不會超過![]() ):
):
空氣質量指數 |
|
|
|
|
|
|
空氣質量等級 |
|
|
|
|
|
|
該社團將該校區(qū)在![]() 年
年![]() 天的空氣質量指數監(jiān)測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
天的空氣質量指數監(jiān)測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
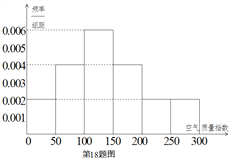
(Ⅰ)請估算![]() 年(以
年(以![]() 天計算)全年空氣質量優(yōu)良的天數(未滿一天按一天計算);
天計算)全年空氣質量優(yōu)良的天數(未滿一天按一天計算);
(Ⅱ)該校![]() 年
年![]() 月
月![]() 、
、![]() 日將作為高考考場,若這兩天中某天出現
日將作為高考考場,若這兩天中某天出現![]() 級重度污染,需要凈化空氣費用
級重度污染,需要凈化空氣費用![]() 元,出現
元,出現![]() 級嚴重污染,需要凈化空氣費用
級嚴重污染,需要凈化空氣費用![]() 元,記這兩天凈化空氣總費用為
元,記這兩天凈化空氣總費用為![]() 元,求
元,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2+ax﹣6a2≤0},B={x||x﹣2|<a},
(1)當a=1時,求A∩B和A∪B;
(2)當BA時,求實數a的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com