【題目】已知圓C:
.
（1）若圓C的切線在x軸和y軸上的截距相等，且截距不為零，求此切線的方程；
（2）從圓C外一點P
向該圓引一條切線，切點為M，O為坐標原點，且有
，
求使得
取得最小值的點P的坐標
【答案】（1）x＋y＋1＝0或x＋y－3＝0；（2）點P的坐標為
.
【解析】
本題考查用點斜式、斜截式求直線方程的方法，體現了分類討論的數學思想，點到直線的距離公式，判斷P在直線2x-4y+3=0上，|PM|的最小值就是|PO|的最小值，時間誒體的關鍵．
（1）當截距不為零時：設切線方程為
，根據圓心到切線的距離等于半徑求出a的值，即得切線方程，當截距等于零時：設切線方程為y=kx（k≠0），同理可得k=2±
，從而得到圓的所有的切線方程．
（2）有切線的性質可得|PM|2=|PC|2-|CM|2，又|PM|=|PO|，可得2x0-4y0+3=0．動點P在直線2x-4y+3=0上，|PM|的最小值就是|PO|的最小值，過點O作直線2x-4y+3=0的垂線，垂足為P，垂足坐標即為所求．
（1）
切線在兩坐標軸上的截距相等且截距不為零，
設切線方程為
，（
）
又圓C：
，圓心C
到切線的距離等于圓的半
徑
， 
則所求切線的方程為：
。
（2）切線PM與半徑CM垂直， 
動點P的軌跡是直線
，
的最小值就是
的最小
值，而的最小值為O到直線的距離d=
，
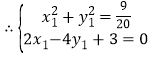
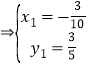
所求點坐標為P
.
全優點練單元計劃系列答案科目：高中數學 來源： 題型：
【題目】公司生產一種電子儀器的固定成本為20000元，每生產一臺儀器需增加投入100元，已知總收益滿足函數：
其中 
x 是儀器的月產量.
（1）將利潤
表示為月產量 
的函數；
（2）當月產量 為何值時，公司所獲利潤最大？最大利潤是多少元？（總收益=總成本+利潤）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C：y2=2px（p＞0）上橫坐標為4的點到焦點的距離為5．
（1）求拋物線C的方程；
（2）設直線y=kx+b與拋物線C交于A（x1 ， y1），B（x2 ， y2），且|y1﹣y2|=2，過弦AB中點M作平行于x軸的直線交拋物線于點D，求△ABD的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
，其中
是實數．
(l）若
，求函數
的單調區間；
(2）當
時，若
為函數
圖像上一點，且直線
與
相切于點
，其中
為坐標原點，求
的值；
(3) 設定義在
上的函數
在點
處的切線方程為
，若
在定義域
內恒成立，則稱函數
具有某種性質
，簡稱“
函數”．當
時，試問函數
是否為“
函數”？若是，請求出此時切點
的橫坐標；若不是，清說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在（0，+∞）上的函數f（x），如果對任意x∈（0，+∞），恒有f（kx）=kf（x），（k≥2，k∈N+）成立，則稱f（x）為k階縮放函數．
（1）已知函數f（x）為二階縮放函數，且當x∈（1，2]時，f（x）=1+ 
x，求f（2 
）的值；
（2）已知函數f（x）為二階縮放函數，且當x∈（1，2]時，f（x）= 
，求證：函數y=f（x）﹣x在（1，+∞）上無零點；
（3）已知函數f（x）為k階縮放函數，且當x∈（1，k]時，f（x）的取值范圍是[0，1），求f（x）在（0，kn+1]（n∈N）上的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
