
【題目】設三棱錐![]() 的每個頂點都在球
的每個頂點都在球![]() 的球面上,
的球面上,![]() 是面積為
是面積為![]() 的等邊三角形,
的等邊三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
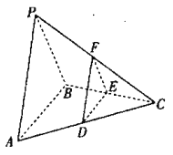
(1)確定![]() 的位置(需要說明理由),并證明:平面
的位置(需要說明理由),并證明:平面![]() 平面
平面![]() .
.
(2)與側面![]() 平行的平面
平行的平面![]() 與棱
與棱![]() ,
,![]() ,
,![]() 分別交于
分別交于![]() ,
,![]() ,
,![]() ,求四面體
,求四面體![]() 的體積的最大值.
的體積的最大值.
【答案】(1)![]() 在
在![]() 上,理由見解析,證明見解析,(2)
上,理由見解析,證明見解析,(2)![]()
【解析】
(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,可證
,可證![]() 在線段
在線段![]() 上,
上,![]() 且
且![]() 平面
平面![]() ,從而得到平面
,從而得到平面![]() 平面
平面![]() .
.
(2)設![]() ,可證
,可證![]() ,利用導數可求體積的最大值.
,利用導數可求體積的最大值.
(1)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,取點
,取點![]() 為
為![]() 的三等分點且
的三等分點且![]() ,
,
連接![]() .
.
因為![]() ,所以
,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,故
,故![]() .
.
因為![]() 為等腰直角三角形,
為等腰直角三角形,![]() 為
為![]() 的中點,故
的中點,故![]() ,
,
因為![]() ,
,![]() ,
,
故![]() ,故
,故![]() ,同理
,同理![]() ,
,
因為![]() 是等邊三角形,故
是等邊三角形,故![]() 為
為![]() 的中心,故
的中心,故![]() ,
,
故![]() 為三棱錐
為三棱錐![]() 的外接球的球心,
的外接球的球心,
故![]() 與
與![]() 重合即
重合即![]() 在線段
在線段![]() 上且
上且![]() .
.

因為![]() 在
在![]() 上,所以
上,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由題意得![]() ,解得
,解得![]() ,
,
因為![]() 為等腰直角三角形,
為等腰直角三角形,![]() 為
為![]() 的中點,故
的中點,故![]() ,
,
而平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() 為點
為點![]() 到平面
到平面![]() 的距離.
的距離.
在等腰直角三角形![]() 中,
中,![]() 即
即![]() 到平面
到平面![]() 的距離
的距離![]() .
.
設![]() ,
,![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
故![]() ,同理
,同理![]() ,因為
,因為![]() 方向相同,故
方向相同,故![]() ,
,
同理![]() ,
,
所以![]() ,則
,則![]() 的面積為
的面積為![]() .
.
又![]() ,所以
,所以![]() 到平面
到平面![]() 的距離為
的距離為![]() ,
,
所以四面體![]() 的體積
的體積![]() .
.
設![]() ,
,![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以![]() 在
在![]() 為增函數,在
為增函數,在![]() 為減函數,
為減函數,
所以![]() ,
,
即四面體![]() 的體積的最大值為
的體積的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】隨著經濟全球化、信息化的發展,企業之間的競爭從資源的爭奪轉向人才的競爭,吸引、留住培養和用好人才成為人力資源管理的戰略目標和緊迫任務,在此背景下,某信息網站在15個城市中對剛畢業的大學生的月平均收入薪資和月平均期望薪資做了調查,數據如下圖所示.
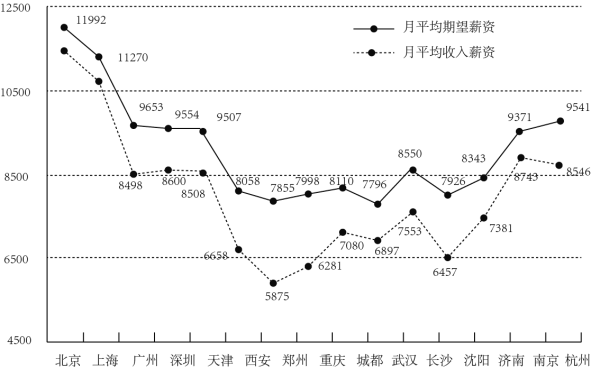
(1)若某大學畢業生從這15座城市中隨機選擇一座城市就業,求該生選中月平均收入薪資高于8500元的城市的概率;
(2)現有2名大學畢業生在這15座城市中各隨機選擇一座城市就業,且2人的選擇相互獨立,記X為選中月平均收入薪資高于8500元的城市的人數,求X的分布列和數學期望E(X);
(3)記圖中月平均收入薪資對應數據的方差為![]() ,月平均期望薪資對應數據的方差為
,月平均期望薪資對應數據的方差為![]() ,判斷
,判斷![]() 與
與![]() 的大小(只需寫出結論)
的大小(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖三棱錐A-BCD中,BD⊥CD,E,F分別為棱BC,CD上的點,且BD∥平面AEF,AE⊥平面BCD.
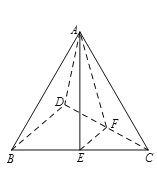
(1)求證:平面AEF⊥平面ACD;
(2)若![]() ,
,![]() 為
為![]() 的中點,求直線
的中點,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與拋物線
與拋物線![]() :
:![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() 的面積為16(
的面積為16(![]() 為坐標原點).
為坐標原點).
(1)求![]() 的方程;
的方程;
(2)直線![]() 經過
經過![]() 的焦點
的焦點![]() 且
且![]() 不與
不與![]() 軸垂直,與
軸垂直,與![]() 交于
交于![]() ,
,![]() 兩點,若線段
兩點,若線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在橢圓![]() 上任取一點
上任取一點![]() (
(![]() 不為長軸端點),連結
不為長軸端點),連結![]() 、
、![]() ,并延長與橢圓
,并延長與橢圓![]() 分別交于點
分別交于點![]() 、
、![]() 兩點,已知
兩點,已知![]() 的周長為8,
的周長為8,![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設坐標原點為![]() ,當
,當![]() 不是橢圓的頂點時,直線
不是橢圓的頂點時,直線![]() 和直線
和直線![]() 的斜率之積是否為定值?若是定值,請求出這個定值;若不是定值,請說明理由.
的斜率之積是否為定值?若是定值,請求出這個定值;若不是定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() 為等腰直角三角形,
為等腰直角三角形,![]() 為等邊三角形,其中O為BC中點,且
為等邊三角形,其中O為BC中點,且![]() .
.
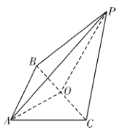
(1)求證:平面![]() 平面PBC;
平面PBC;
(2)若![]() 且
且![]() 平面EBC,其中E為AP上的點,求CE與平面ABC所成角的正弦值.
平面EBC,其中E為AP上的點,求CE與平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 、
、![]() 與平面
與平面![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,
,![]() ,則下列命題中正確的是( )
,則下列命題中正確的是( )
A.![]() 是
是![]() 的充分不必要條件
的充分不必要條件
B.![]() 是
是![]() 的充要條件
的充要條件
C.設![]() ,則
,則![]() 是
是![]() 的必要不充分條件
的必要不充分條件
D.設![]() ,則
,則![]() 是
是![]() 的既不充分也不必要條件
的既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com