
【題目】已知函數![]() ,
,![]() 為其導函數,且
為其導函數,且![]() 時
時![]() 有極小值-9.
有極小值-9.
(1)求![]() 的單調遞減區間;
的單調遞減區間;
(2)若![]() ,
,![]() ,當
,當![]() 時,對于任意
時,對于任意![]() ,
,![]() 和
和![]() 的值至少有一個是正數,求實數
的值至少有一個是正數,求實數![]() 的取值范圍;
的取值范圍;
(3)若不等式![]() (
(![]() 為正整數)對任意正實數
為正整數)對任意正實數![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)先求函數的解析式,再運用導數求解;
(2)借助題設條件分類分析推證求解;
(3)借助題設構造函數,運用分析推證的方法求解.
試題解析:
(1)由![]() ,因為函數在
,因為函數在![]() 時有極小值-9,
時有極小值-9,
所以![]() ,從而得
,從而得![]() ,
,![]() ,
,
所求的![]() ,所以
,所以![]() ,
,
由![]() 解得
解得![]() ,所以
,所以![]() 的單調遞減區間為(-1,3).
的單調遞減區間為(-1,3).
(2)由![]() ,故
,故![]() ,
,
當![]() 時,若
時,若![]() ,則
,則![]() ,滿足條件;
,滿足條件;
若![]() ,則
,則![]() ,滿足條件;
,滿足條件;
若![]() ,
,![]() .
.
①如果對稱軸![]() ,即
,即![]() 時,
時,![]() 的開口向上,
的開口向上,
故在![]() 上單調遞減,又
上單調遞減,又![]() ,所以當
,所以當![]() 時,
時,![]() .
.
②如果對稱軸![]() ,即
,即![]() 時,
時,![]() ,
,
解得![]() ,故
,故![]() 時,
時,![]() ;
;
所以![]() 的取值范圍為
的取值范圍為![]() ;
;
(3)因為![]() ,所以
,所以![]() 等價于
等價于
![]() ,即
,即![]() ,
,
記![]() ,則
,則![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]() ,
,
![]() 對任意正實數
對任意正實數![]() 恒成立,等價于
恒成立,等價于![]() ,即
,即![]() ,
,
記![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上單調遞減,又
上單調遞減,又![]() ,
,![]() ,
,
所以![]() 的最大值為6.
的最大值為6.


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:
【題目】中國乒乓球隊備戰里約奧運會熱身賽暨選拔賽于2016年7月14日在山東威海開賽.種子選手![]() 與
與![]() ,
,![]() ,
,![]() 三位非種子選手分別進行一場對抗賽,按以往多次比賽的統計,
三位非種子選手分別進行一場對抗賽,按以往多次比賽的統計,![]() 獲勝的概率分別為
獲勝的概率分別為![]() ,
,![]() ,
,![]() ,且各場比賽互不影響.
,且各場比賽互不影響.
(1)若![]() 至少獲勝兩場的概率大于
至少獲勝兩場的概率大于![]() ,則
,則![]() 入選征戰里約奧運會的最終大名單,否則不予入選,問
入選征戰里約奧運會的最終大名單,否則不予入選,問![]() 是否會入選最終的大名單?
是否會入選最終的大名單?
(2)求![]() 獲勝場數
獲勝場數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數25,規定第1次操作為23+53=133,第2次操作為13+33+33=55,如此反復操作,則第2 017次操作后得到的數是( )
A. 25 B. 250
C. 55 D. 133
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,當點
,當點![]() 在
在![]() 的圖象上運動時,點
的圖象上運動時,點![]() 在函數
在函數![]() 的圖象上運動(
的圖象上運動(![]() ).
).
(Ⅰ)求![]() 和
和![]() 的表達式;
的表達式;
(Ⅱ)已知關于![]() 的方程
的方程![]() 有實根,求實數
有實根,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)設![]() ,函數
,函數![]() 的值域為
的值域為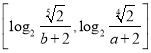 ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將編號為1,2,3,4,5的五個球放入編號為1,2,3,4,5的五個盒子里,每個盒子內放一個球,若恰好有三個球的編號與盒子編號相同,則不同投放方法的種數為( )
A.6 B.10
C.20 D.30
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com