
【題目】已知函數![]()
(1)若函數![]() 在
在![]() 處有極值為10,求
處有極值為10,求![]() 的值;
的值;
(2)對任意![]() ,
,![]() 在區間
在區間![]() 單調增,求
單調增,求![]() 的最小值;
的最小值;
(3)若![]() ,且過點
,且過點![]() 能作
能作![]() 的三條切線,求
的三條切線,求![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)根據![]() 列方程組,解方程組求得
列方程組,解方程組求得![]() 的值.(2)依題意得
的值.(2)依題意得![]() 對
對![]() ,當
,當![]() 恒成立,構造函數
恒成立,構造函數![]() ,利用一次函數的單調性求得
,利用一次函數的單調性求得![]() .再構造函數
.再構造函數![]() ,根據二次函數的對稱軸得
,根據二次函數的對稱軸得![]() ,由此求得
,由此求得![]() 的最小值.(3)當
的最小值.(3)當![]() 時,
時,![]() ,設出切點的坐標,利用導數求得切線的斜率列方程并化簡,構造函數記
,設出切點的坐標,利用導數求得切線的斜率列方程并化簡,構造函數記![]() ,根據過點
,根據過點![]() ,能作
,能作![]() 的三條切線可知
的三條切線可知![]() 有三個零點,利用
有三個零點,利用![]() 的導數求得
的導數求得![]() 的極大值和極小值,由此列不等式組,解不等式組求得
的極大值和極小值,由此列不等式組,解不等式組求得![]() 的取值范圍.
的取值范圍.
解:(1)![]() ,依題意:
,依題意:
![]() ①,
①,![]() ②
②
由①②解得:![]() ,或
,或![]() ;
;
經檢驗當![]() 時無極值點,
時無極值點,
當![]() 時函數
時函數![]() 在
在![]() 處有極小值,故
處有極小值,故![]() ,
,
(2)![]() 對
對![]() ,當
,當![]() 恒成立
恒成立
記![]() ,
,
∴![]()
又設![]() ,
,
當![]() 時
時![]() ,
,
![]() ,∴
,∴![]() 的最小值為
的最小值為![]() ,
,
(3):當![]() 時,
時,![]() ,
,
設切點為![]() ,則切線斜率為
,則切線斜率為![]() ,
,
∴![]() ,
,
記![]() ,
,
過點![]() 能作
能作![]() 三條切線等價于
三條切線等價于![]() 有三個零點
有三個零點
![]()
|
|
|
|
| 正 | 負 | 正 |
| 增 | 減 | 增 |
令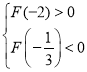 ,即
,即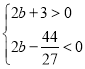 ,
,
∴![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,若函數
,若函數![]() 有三個不同的零點
有三個不同的零點![]() ,
,![]() ,
,![]() (其中
(其中![]() ),則
),則![]() 的取值范圍為__________.
的取值范圍為__________.
【答案】![]()
【解析】如圖:

![]() ,
,![]() ,作出函數圖象如圖所示
,作出函數圖象如圖所示
![]() ,
,![]() ,作出函數圖象如圖所示
,作出函數圖象如圖所示
![]()
![]() ,由
,由![]() 有三個不同的零點
有三個不同的零點
![]() ,如圖
,如圖
令![]()
![]()
得![]()
![]()
為滿足有三個零點,如圖可得
![]() ,
,![]()
![]()
![]()
點睛:本題考查了函數零點問題,先由導數求出兩個函數的單調性,繼而畫出函數圖像,再由函數的零點個數確定參量取值范圍,將問題轉化為函數的兩根問題來求解,本題需要化歸轉化,函數的思想,零點問題等較為綜合,有很大難度。
【題型】填空題
【結束】
17
【題目】已知等比數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某少數民族的刺繡有著悠久的歷史,如圖4①,②,③,④為她們刺繡最簡單的四個圖案,這些圖案都是由小正方形構成,小正方形數越多刺繡越漂亮.現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含f(n)個小正方形.
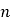
(1)求出f(5)的值;
(2)利用合情推理的“歸納推理思想”,歸納出f(n+1)與f(n)之間的關系式,并根據你得到的關系式求出f(n)的表達式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量a=(3sinα,cosα),b=(2sinα,5sinα-4cosα),α∈![]() ,且a⊥b.
,且a⊥b.
(1)求tanα的值;
(2)求cos![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了估計某校某次數學考試的情況,現從該校參加考試的600名學生中隨機抽出60名學生,其數學成績(百分制)均在![]() 內,將這些成績分成六組
內,將這些成績分成六組![]() …
…![]() ,得到如圖所示的部分頻率分布直方圖.
,得到如圖所示的部分頻率分布直方圖.

(1)求抽出的60名學生中數學成績在![]() 內的人數;
內的人數;
(2)若規定成績不小于85分為優秀,則根據頻率分布直方圖,估計該校參加考試的學生數學成績為優秀的人數;
(3)試估計抽出的60名學生的數學成績的中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,霧霾日趨嚴重,霧霾的工作、生活受到了嚴重的影響,如何改善空氣質量已成為當今的熱點問題,某空氣凈化器制造廠,決定投入生產某型號的空氣凈化器,根據以往的生產銷售經驗得到下面有關生產銷售的統計規律,每生產該型號空氣凈化器![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為12萬元,并且每生產1百臺的生產成本為10萬元(總成本=固定成本+生產成本),銷售收入
(萬元),其中固定成本為12萬元,并且每生產1百臺的生產成本為10萬元(總成本=固定成本+生產成本),銷售收入![]() (萬元)滿足
(萬元)滿足![]() ,假定該產品銷售平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
,假定該產品銷售平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
(1)求利潤函數![]() 的解析式(利潤=銷售收入-總成本);
的解析式(利潤=銷售收入-總成本);
(2)工廠生產多少百臺產品時,可使利潤最多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com