
【題目】在數(shù)列{an}中,a1=1,且anan+1+ ![]() (an﹣an+1)+1=0,則a2016=( )
(an﹣an+1)+1=0,則a2016=( )
A.1
B.﹣1
C.2+ ![]()
D.2﹣ ![]()
【答案】D
【解析】解:∵anan+1+ ![]() (an﹣an+1)+1=0,
(an﹣an+1)+1=0,
∴( ![]() ﹣an)an+1=
﹣an)an+1= ![]() an+1,
an+1,
∴an+1= ![]() ,
,
∵a1=1,
∴a2= ![]() =2+
=2+ ![]() ,
,
∴a3= ![]() =﹣2﹣
=﹣2﹣ ![]() ,
,
∴a4= ![]() =﹣1,
=﹣1,
∴a5= ![]() =﹣2+
=﹣2+ ![]() ,
,
∴a6= ![]() =2﹣
=2﹣ ![]() ,
,
∴a7= ![]() =1,
=1,
∴數(shù)列{an}是以6為周期的擺動數(shù)列,
∴a2016=a6×336=a6=2﹣ ![]()
故選:D.
【考點(diǎn)精析】通過靈活運(yùn)用數(shù)列的通項(xiàng)公式,掌握如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項(xiàng)公式即可以解答此題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了調(diào)查患胃病是否與生活規(guī)律有關(guān),在某地對![]() 名
名![]() 歲以上的人進(jìn)行了調(diào)查,結(jié)果是:患胃病者生活不規(guī)律的共
歲以上的人進(jìn)行了調(diào)查,結(jié)果是:患胃病者生活不規(guī)律的共![]() 人,患胃病者生活規(guī)律的共
人,患胃病者生活規(guī)律的共![]() 人,未患胃病者生活不規(guī)律的共
人,未患胃病者生活不規(guī)律的共![]() 人,未患胃病者生活規(guī)律的共
人,未患胃病者生活規(guī)律的共![]() 人.
人.
(1)根據(jù)以上數(shù)據(jù)列出![]() 列聯(lián)表;
列聯(lián)表;
(2)能否在犯錯誤的概率不超過![]() 的前提下認(rèn)為“
的前提下認(rèn)為“![]() 歲以上的人患胃病與否和生活規(guī)律有關(guān)系?”
歲以上的人患胃病與否和生活規(guī)律有關(guān)系?”
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某污水處理廠要在一個矩形污水處理池(ABCD)的池底水平鋪設(shè)污水凈化管道(管道構(gòu)成Rt△FHE,H是直角項(xiàng)點(diǎn))來處理污水.管道越長,污水凈化效果越好.設(shè)計要求管道的接口H是AB的中點(diǎn),E,F(xiàn)分別落在線段BC,AD上.已知AB=20米,AD=![]() 米,記∠BHE=
米,記∠BHE=![]() .
.

(1)試將污水凈化管道的長度L表示為![]() 的函數(shù),并寫出定義域;
的函數(shù),并寫出定義域;
(2)當(dāng)![]() 取何值時,污水凈化效果最好?并求出此時管道的長度L.
取何值時,污水凈化效果最好?并求出此時管道的長度L.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a,b,c分別為△ABC三個內(nèi)角A,B,C所對的邊長,且acosB﹣bcosA= ![]() c.
c.
(Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)若A=60°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】執(zhí)行如圖的程序框圖,若輸出的y值為5,則判斷框中可填入的條件是( ) 
A.i<3
B.i<4
C.i<5
D.i<6
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】古希臘著名數(shù)學(xué)家阿波羅尼斯與歐幾里得、阿基米德齊名.他發(fā)現(xiàn):“平面內(nèi)到兩個定點(diǎn)![]() 的距離之比為定值
的距離之比為定值![]() 的點(diǎn)的軌跡是圓”.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓在平面直角坐標(biāo)系
的點(diǎn)的軌跡是圓”.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓在平面直角坐標(biāo)系![]() 中,
中,![]() 點(diǎn)
點(diǎn)![]() .設(shè)點(diǎn)
.設(shè)點(diǎn)![]() 的軌跡為
的軌跡為![]() ,下列結(jié)論正確的是( )
,下列結(jié)論正確的是( )
A. ![]() 的方程為
的方程為![]()
B. 在![]() 軸上存在異于
軸上存在異于![]() 的兩定點(diǎn)
的兩定點(diǎn)![]() ,使得
,使得![]()
C. 當(dāng)![]() 三點(diǎn)不共線時,射線
三點(diǎn)不共線時,射線![]() 是
是![]() 的平分線
的平分線
D. 在![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
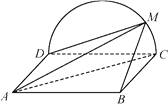
【題目】如圖,邊長為2的正方形![]() 所在的平面與半圓弧
所在的平面與半圓弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上異于
上異于![]() ,
,![]() 的點(diǎn).
的點(diǎn).
(1)證明:平面![]() 平面
平面![]() ;
;
(2)當(dāng)三棱錐![]() 體積最大時,求面
體積最大時,求面![]() 與面
與面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)有![]() 、
、![]() 兩個崗位招聘大學(xué)畢業(yè)生,其中第一天收到這兩個崗位投簡歷的大學(xué)生人數(shù)如下表:
兩個崗位招聘大學(xué)畢業(yè)生,其中第一天收到這兩個崗位投簡歷的大學(xué)生人數(shù)如下表:
|
| 總計 | |
女生 | 12 | 8 | 20 |
男生 | 24 | 56 | 80 |
總計 | 36 | 64 | 100 |
(1)根據(jù)以上數(shù)據(jù)判斷是有![]() 的把握認(rèn)為招聘的
的把握認(rèn)為招聘的![]() 、
、![]() 兩個崗位與性別有關(guān)?
兩個崗位與性別有關(guān)?
(2)從投簡歷的女生中隨機(jī)抽取兩人,記其中投![]() 崗位的人數(shù)為
崗位的人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
參考公式:![]() ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com