
【題目】某同學用“五點法”畫函數![]() 在某一周期內的圖象時,列表并填入了部分數據,如下表:
在某一周期內的圖象時,列表并填入了部分數據,如下表:
|
|
|
|
|
|
|
| ① |
| ||
|
|
|
|
|
|
(1)請將上面表格中①的數據填寫在答題卡相應位置上,并直接寫出函數![]() 的解析式;
的解析式;
(2)若將函數![]() 的圖象上所有點的橫坐標變為原來的
的圖象上所有點的橫坐標變為原來的![]() 倍,縱坐標不變,得到函數
倍,縱坐標不變,得到函數![]() 的圖象,求當
的圖象,求當![]() 時,函數
時,函數![]() 的單調遞增區間;
的單調遞增區間;
(3)若將函數![]() 圖象上的所有點向右平移
圖象上的所有點向右平移![]() 個單位長度,得到
個單位長度,得到![]() 的圖象. 若
的圖象. 若![]() 圖象的一個對稱中心為
圖象的一個對稱中心為![]() ,求
,求![]() 的最小值.
的最小值.
 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:
【題目】設數列{an}滿足![]() .
.
(1)若![]() ,求證:存在
,求證:存在![]() (a,b,c為常數),使數列
(a,b,c為常數),使數列![]() 是等比數列,并求出數列{an}的通項公式;
是等比數列,并求出數列{an}的通項公式;
(2)若an 是一個等差數列{bn}的前n項和,求首項a1的值與數列{bn}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某親子游戲結束時有一項抽獎活動,抽獎規則是:盒子里面共有4個小球,小球上分別寫有0,1,2,3的數字,小球除數字外其他完全相同,每對親子中,家長先從盒子中取出一個小球,記下數字后將小球放回,孩子再從盒子中取出一個小球,記下小球上數字將小球放回.抽獎活動的獎勵規則是:①若取出的兩個小球上數字之積大于4,則獎勵飛機玩具一個;②若取出的兩個小球上數字之積在區間上![]() ,則獎勵汽車玩具一個;③若取出的兩個小球上數字之積小于1,則獎勵飲料一瓶.
,則獎勵汽車玩具一個;③若取出的兩個小球上數字之積小于1,則獎勵飲料一瓶.
(1)求每對親子獲得飛機玩具的概率;
(2)試比較每對親子獲得汽車玩具與獲得飲料的概率,哪個更大?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)求函數![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .(Ⅱ)當
.(Ⅱ)當![]() 時,
時, ![]()
![]() ;當
;當![]() 時,
時, ![]()
![]() .
.
【解析】【試題分析】(I)利用![]() 的二階導數來研究求得函數
的二階導數來研究求得函數![]() 的單調區間.(II) 由(Ⅰ)得
的單調區間.(II) 由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,由此可知
上單調遞增,由此可知![]() .利用導數和對
.利用導數和對![]() 分類討論求得函數在
分類討論求得函數在![]() 不同取值時的最大值.
不同取值時的最大值.
【試題解析】
(Ⅰ)![]() ,
,
設![]()
![]() ,則
,則![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
從而得![]() 在
在![]() 上單調遞增,又∵
上單調遞增,又∵![]() ,
,
∴當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
因此, ![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
(Ⅱ)由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
由此可知![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
設![]() ,
,
則![]()
![]()
 .
.
∵當![]() 時,
時, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
又∵![]() ,∴當
,∴當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
①當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() ;
;
②當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() .
.
綜上, ![]() 在
在![]() 上的最大值為:當
上的最大值為:當![]() 時,
時, ![]()
![]() ;
;
當![]() 時,
時, ![]()
![]() .
.
[點睛]本小題主要考查函數的單調性,考查利用導數求最大值. 與函數零點有關的參數范圍問題,往往利用導數研究函數的單調區間和極值點,并結合特殊點,從而判斷函數的大致圖像,討論其圖象與![]() 軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
【題型】解答題
【結束】
22
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,圓
中,圓![]() 的普通方程為
的普通方程為![]() . 在以坐標原點為極點,
. 在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ) 寫出圓 ![]() 的參數方程和直線
的參數方程和直線![]() 的直角坐標方程;
的直角坐標方程;
( Ⅱ ) 設直線![]() 與
與![]() 軸和
軸和![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() 為圓
為圓![]() 上的任意一點,求
上的任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次“漢馬”(武漢馬拉松比賽的簡稱)全程比賽中,50名參賽選手(24名男選手和26名女選手)的成績(單位:分鐘)分別為數據![]() (成績不為0).
(成績不為0).
(Ⅰ)24名男選手成績的莖葉圖如圖⑴所示,若將男選手成績由好到差編為1~24號,再用系統抽樣方法從中抽取6人,求其中成績在區間![]() 上的選手人數;
上的選手人數;

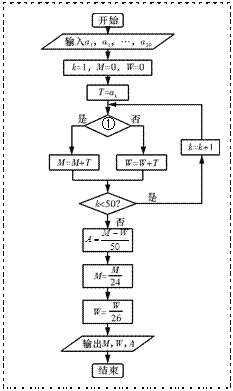
(Ⅱ)如圖⑵所示的程序用來對這50名選手的成績進行統計.為了便于區別性別,輸入時,男選手的成績數據用正數,女選手的成績數據用其相反數(負數),請完成圖⑵中空白的判斷框①處的填寫,并說明輸出數值![]() 和
和![]() 的統計意義.
的統計意義.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市隨機抽取一年(365天)內100天的空氣質量指數![]() 的監測數據,結果統計如下:
的監測數據,結果統計如下:

記某企業每天由空氣污染造成的經濟損失![]() (單位:元),空氣質量指數
(單位:元),空氣質量指數![]() 為
為![]() .當
.當![]() 時,企業沒有造成經濟損失;當
時,企業沒有造成經濟損失;當![]() 對企業造成經濟損失成直線模型(當
對企業造成經濟損失成直線模型(當![]() 時造成的經濟損失為
時造成的經濟損失為![]() ,當
,當![]() 時,造成的經濟損失
時,造成的經濟損失![]() ;當
;當![]() 時造成的經濟損失為2000元;
時造成的經濟損失為2000元;
(1)試寫出![]() 的表達式:
的表達式:
(2)在本年內隨機抽取一天,試估計該天經濟損失超過350元的概率;
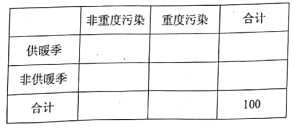
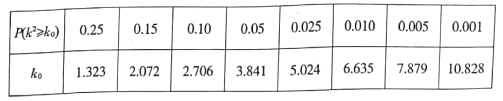
(3)若本次抽取的樣本數據有30天是在供暖季,其中有12天為重度污染,完成下面![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為該市本年空氣重度污染與供暖有關?
的把握認為該市本年空氣重度污染與供暖有關?
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系中,直線![]() 的參數方程為
的參數方程為![]() ,(
,(![]() 為參數).以原點為極點,
為參數).以原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的極坐標方程與曲線
的極坐標方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知與直線![]() 平行的直線
平行的直線![]() 過點
過點![]() ,且與曲線
,且與曲線![]() 交于
交于![]() 兩點,試求
兩點,試求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【題目】已知拋物線C:y2=2x,過點(2,0)的直線l交C于A,B兩點,圓M是以線段AB為直徑的圓.
(1)證明:坐標原點O在圓M上;
(2)設圓M過點P(4,-2),求直線l與圓M的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com