
【題目】已知函數 ![]() .
.
(1)求證:函數f(x)在實數集R上為增函數;
(2)設g(x)=log2f(x),若關于x的方程g(x)=a有解,求實數a的取值范圍.
【答案】
(1)證明:由題意知, ![]() ,
,
設x1,x2是R上的任意兩個數,且x1<x2,
則 ![]()
= 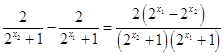 ,
,
因為x1<x2,所以 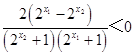 ,
,
即f(x1)<f(x2),
所以f(x)在R上為增函數
(2)解:因為關于x的方程g(x)=a有解,
所以實數a的取值范圍為函數y=g(x)的值域;
因為 ![]() ,
,
因為2x+1>1,所以 ![]() ,
,
即0<f(x)<2
所以g(x)=log2f(x)值域為(﹣∞,1),
即實數a的取值范圍為(﹣∞,1)
【解析】(1)先化簡解析式,再利用函數單調性的定義:取值、作差、變形、定號、下結論,證明函數的單調性;(2)將方程有解轉化為求出函數y=g(x)的值域,由指數函數的性質求出f(x)的范圍,由對數函數的性質求出g(x)的值域,即可求出實數a的取值范圍.
【考點精析】利用奇偶性與單調性的綜合對題目進行判斷即可得到答案,需要熟知奇函數在關于原點對稱的區間上有相同的單調性;偶函數在關于原點對稱的區間上有相反的單調性.


 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,若對于在定義域內存在實數
,若對于在定義域內存在實數![]() 滿足
滿足![]() ,則稱函數
,則稱函數![]() 為“局部奇函數”.若函數
為“局部奇函數”.若函數![]() 是定義在
是定義在![]() 上的“局部奇函數”,則實數
上的“局部奇函數”,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. [1﹣![]() ,1+
,1+![]() ) B. [﹣1,2] C. [﹣2
) B. [﹣1,2] C. [﹣2![]() ,2
,2![]() ] D. [﹣2
] D. [﹣2![]() ,1﹣
,1﹣![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改進后生產甲產品過程中記錄的產量x(噸)與相應的生產能耗y(噸標準煤)的幾組對照數據.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)請根據上表提供的數據,用最小二乘法求出y關于x的回歸方程 ![]() ;
;
(2)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(1)求出的回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
(參考數值:3×2.5+4×3+5×4+6×4.5=66.5)計算回歸系數 ![]() ,
, ![]() .公式為
.公式為  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2, ![]() =λ
=λ ![]() .
. 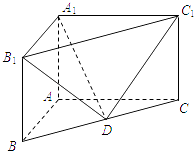
(1)若λ=1,求直線DB1與平面A1C1D所成角的正弦值;
(2)若二面角B1﹣A1C1﹣D的大小為60°,求實數λ的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com