
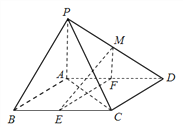
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,側面
,側面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)如果直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
【答案】(Ⅰ)詳見解析(Ⅱ)![]()
【解析】試題分析:(Ⅰ)線面垂直的證明,往往利用線面垂直判定定理,即從線線垂直出發(fā)給予證明,而線線垂直的尋找與論證,一般從兩個方面,一是利用平幾知識,如本題經(jīng)解三角形可得![]() ,再根據(jù)中點條件得平行條件,從而可得
,再根據(jù)中點條件得平行條件,從而可得![]() .二是利用線面位置關系有關定理進行轉化,如本題利用面面垂直的性質定理可得線面垂直,再根據(jù)線面垂直性質定理可得線線垂直.(Ⅱ)解決有關線面角的問題,一般利用空間向量數(shù)量積進行處理比較方便,先根據(jù)條件建立空間直角坐標系,設立各點坐標,利用方程組解出面的法向量,再根據(jù)向量數(shù)量積求出直線向量與法向量夾角余弦值,最后根據(jù)線面角與向量夾角之間關系列等量關系,求出比值.
.二是利用線面位置關系有關定理進行轉化,如本題利用面面垂直的性質定理可得線面垂直,再根據(jù)線面垂直性質定理可得線線垂直.(Ⅱ)解決有關線面角的問題,一般利用空間向量數(shù)量積進行處理比較方便,先根據(jù)條件建立空間直角坐標系,設立各點坐標,利用方程組解出面的法向量,再根據(jù)向量數(shù)量積求出直線向量與法向量夾角余弦值,最后根據(jù)線面角與向量夾角之間關系列等量關系,求出比值.
試題解析:
(Ⅰ)證明:在平行四邊形![]() 中,因為
中,因為![]() ,
, ![]() ,
,
所以![]() .由
.由![]() 分別為
分別為![]() 的中點,得
的中點,得![]() ,
,
所以![]() .
.
因為側面![]() 底面
底面![]() ,且
,且![]() ,所以
,所以![]() 底面
底面![]() .
.
又因為![]() 底面
底面![]() ,所以
,所以![]() .
.
又因為![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:因為![]() 底面
底面![]() ,
, ![]() ,所以
,所以![]() 兩兩垂直,
兩兩垂直,
以![]() 分別為
分別為![]() 、
、![]() 、
、![]() ,建立空間直角坐標系,
,建立空間直角坐標系,
則![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
設![]() ,則
,則![]() ,
,
所以![]() ,
, ![]() ,易得平面
,易得平面![]() 的法向量
的法向量![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,由
,由![]() ,
, ![]() ,得
,得![]()
令![]() , 得
, 得![]() .
.
因為直線![]() 與平面
與平面![]() 所成的角和此直線與平面
所成的角和此直線與平面![]() 所成的角相等,
所成的角相等,
所以![]() ,即
,即 ,所以
,所以 ![]() ,
,
解得![]() ,或
,或![]() (舍). 綜上所得:
(舍). 綜上所得: ![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(Ⅰ)若![]() 和
和![]() 在
在![]() 有相同的單調區(qū)間,求
有相同的單調區(qū)間,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)令![]() (
(![]() ),若
),若![]() 在定義域內有兩個不同的極值點.
在定義域內有兩個不同的極值點.
(i)求![]() 的取值范圍;
的取值范圍;
(ii)設兩個極值點分別為![]() ,
, ![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 定義域為
定義域為![]() ,對任意
,對任意![]() 都有
都有![]() ,且當
,且當![]() 時,
時, ![]() .
.
(1)試判斷![]() 的單調性,并證明;
的單調性,并證明;
(2)若![]() ,
,
①求![]() 的值;
的值;
②求實數(shù)![]() 的取值范圍,使得方程
的取值范圍,使得方程![]() 有負實數(shù)根.
有負實數(shù)根.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,且點
,且點![]() 在橢圓
在橢圓![]() 上.
上.
⑴求橢圓![]() 的標準方程;
的標準方程;
⑵已知動直線![]() 過點
過點![]() 且與橢圓
且與橢圓![]() 交于
交于![]() 兩點.試問
兩點.試問![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 恒成立?若存在,求出點Q的坐標;若不存在,請說明理由.
恒成立?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有最大值4 和最小值1,設
上有最大值4 和最小值1,設![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在區(qū)間
在區(qū)間![]() 上有解,求實數(shù)
上有解,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() 有三個不同的實數(shù)解,求實數(shù)
有三個不同的實數(shù)解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】各項均為正數(shù)的數(shù)列{an}中,前n項和![]() .
.
(1)求數(shù)列{an}的通項公式;
(2)若![]() 恒成立,求k的取值范圍;
恒成立,求k的取值范圍;
(3)是否存在正整數(shù)m,k,使得am,am+5,ak成等比數(shù)列?若存在,求出m和k的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 是等差數(shù)列,其前
是等差數(shù)列,其前![]() 項和為
項和為![]() ,數(shù)列
,數(shù)列![]() 是公比大于0的等比數(shù)列,且
是公比大于0的等比數(shù)列,且![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求數(shù)列![]() 和
和![]() 的通項公式;
的通項公式;
(Ⅱ)令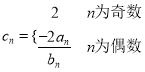 ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和為
項和為![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com