【題目】在四個函數(shù)y=sin|x|，y=cos|x|，y= 
，y=lg|sinx|中，以π為周期，在 
上單調(diào)遞增的偶函數(shù)是（ ）
A.y=sin|x|
B.y=cos|x|
C.y=
D.y=lg|sinx|
【答案】D
【解析】解：由于函數(shù)y=sin|x|不具有周期性，故排除A；
由于函數(shù)y=cos|x|在 
上單調(diào)遞減，故排除B；
由于函數(shù)y= 
在 上單調(diào)遞減，故排除C；
由于函數(shù)y=lg|sinx|的周期為π，且是在 上單調(diào)遞增的偶函數(shù)，故滿足條件，
故選：D．
【考點精析】根據(jù)題目的已知條件，利用函數(shù)奇偶性的性質(zhì)的相關(guān)知識可以得到問題的答案，需要掌握在公共定義域內(nèi)，偶函數(shù)的加減乘除仍為偶函數(shù)；奇函數(shù)的加減仍為奇函數(shù)；奇數(shù)個奇函數(shù)的乘除認為奇函數(shù)；偶數(shù)個奇函數(shù)的乘除為偶函數(shù)；一奇一偶的乘積是奇函數(shù);復(fù)合函數(shù)的奇偶性：一個為偶就為偶，兩個為奇才為奇．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù) 
．
（1）a的值為多少時，f（x）是偶函數(shù)？
（2）若對任意x∈[0，+∞），都有f（x）＞0，求實數(shù)a的取值范圍．
（3）若f（x）在區(qū)間[0，+∞）上單調(diào)遞增，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
， 
．
（Ⅰ）當
時，求函數(shù)
的極值；
（Ⅱ）當
時，討論函數(shù)
單調(diào)性；
（Ⅲ）是否存在實數(shù)
，對任意的
， 
，且
，有
恒成立？若存在，求出
的取值范圍；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】質(zhì)監(jiān)部門從某超市銷售的甲、乙兩種食用油中分別各隨機抽取100桶檢測某項質(zhì)量指標，由檢測結(jié)果得到如下的頻率分布直方圖：
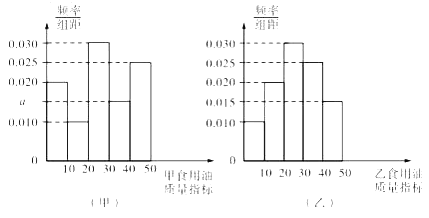
（Ⅰ）寫出頻率分布直方圖（甲）中
的值；記甲、乙兩種食用油100桶樣本的質(zhì)量指標的方差分別為
，
，試比較，的大小（只要求寫出答案）；
（Ⅱ）估計在甲、乙兩種食用油中隨機抽取1捅，恰有一桶的質(zhì)量指標大于20；
（Ⅲ）由頻率分布直方圖可以認為，乙種食用油的質(zhì)量指標值
服從正態(tài)分布
．其中
近似為樣本平均數(shù)
，
近似為樣本方差，設(shè)
表示從乙種食用油中隨機抽取10桶，其質(zhì)量指標值位于（14.55，38.45）的桶數(shù)，求的數(shù)學(xué)期望．
注：①同一組數(shù)據(jù)用該區(qū)問的中點值作代表，計算得
②若
，則
，
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)f（x）=2sin（2x+ 
），g（x）=mcos（2x﹣ 
）﹣2m+3（m＞0），若對任意x1∈[0， 
]，存在x2∈[0， ]，使得g（x1）=f（x2）成立，則實數(shù)m的取值范圍是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】把下列各命題作為原命題，分別寫出它們的逆命題、否命題和逆否命題．
(1)若α＝β，則sin α＝sin β；
(2)若對角線相等，則梯形為等腰梯形；
(3)已知a，b，c，d都是實數(shù)，若a＝b，c＝d，則a＋c＝b＋d.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】對于
維向量
，若對任意
均有
或
，則稱
為
維
向量. 對于兩個
維
向量
定義
.
（1）若
, 求
的值；
（2）現(xiàn)有一個
維
向量序列： 
若
且滿足： 
，求證：該序列中不存在
維
向量
.
(3) 現(xiàn)有一個
維
向量序列： 
若
且滿足： 
，若存在正整數(shù)
使得
為
維
向量序列中的項，求出所有的
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
