
【題目】某企業擬建造如圖所示的容器(不計厚度,長度單位:米),其中容器的中間為圓柱形,左右兩端均為半球形,按照設計要求容器的容積為![]() 立方米,且l≥2r.假設該容器的建造費用僅與其表面積有關,已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為c(c>3)千元.設該容器的建造費用為y千元.
立方米,且l≥2r.假設該容器的建造費用僅與其表面積有關,已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為c(c>3)千元.設該容器的建造費用為y千元.
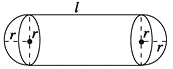
①寫出y關于r的函數表達式,并求該函數的定義域;
②求該容器的建造費用最小時的r.
【答案】①y=4π(c-2)r2+![]() ,0<r≤2②當3<c≤
,0<r≤2②當3<c≤![]() 時,建造費用最小時r=2;當c>
時,建造費用最小時r=2;當c>![]() 時,建造費用最小時,r=
時,建造費用最小時,r=![]() .
.
【解析】(1)由體積V=![]() ,解得l=
,解得l=![]() ,
,
∴y=2πrl×3+4πr2×c
=6πr×![]() +4cπr2
+4cπr2
=2π![]() ,
,
又l≥2r,即![]() ≥2r,解得0<r≤2
≥2r,解得0<r≤2
∴其定義域為(0,2].
(2)由(1)得,y′=8π(c﹣2)r﹣![]() ,
,
=![]() ,0<r≤2
,0<r≤2
由于c>3,所以c﹣2>0
當r3﹣![]() =0時,則r=
=0時,則r=![]()
令![]() =m,(m>0)
=m,(m>0)
所以y′=![]()
①當0<m<2即c>![]() 時,
時,
當r=m時,y′=0
當r∈(0,m)時,y′<0
當r∈(m,2)時,y′>0
所以r=m是函數y的極小值點,也是最小值點.
②當m≥2即3<c≤![]() 時,
時,
當r∈(0,2)時,y′<0,函數單調遞減.
所以r=2是函數y的最小值點.
綜上所述,當3<c≤![]() 時,建造費用最小時r=2;
時,建造費用最小時r=2;
當c>![]() 時,建造費用最小時r=
時,建造費用最小時r=![]()


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知三棱臺ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 
(1)求證:BC1⊥平面AA1C1C
(2)點D是B1C1的中點,求二面角A1﹣BD﹣B1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:集合![]() ,其中
,其中
![]() .
.![]() ,稱
,稱![]() 為
為![]() 的第
的第![]() 個坐標分量.若
個坐標分量.若![]() ,且滿足如下兩條性質:
,且滿足如下兩條性質:
①![]() 中元素個數不少于
中元素個數不少于![]() 個.
個.
②![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 的第
的第![]() 個坐標分量都是
個坐標分量都是![]() .則稱
.則稱![]() 為
為![]() 的一個好子集.
的一個好子集.
(![]() )若
)若![]() 為
為![]() 的一個好子集,且
的一個好子集,且![]() ,
,![]() ,寫出
,寫出![]() ,
,![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集,求證:
的一個好子集,求證:![]() 中元素個數不超過
中元素個數不超過![]() .
.
(![]() )若
)若![]() 為
為![]() 的一個好子集且
的一個好子集且![]() 中恰好有
中恰好有![]() 個元素,求證:一定存在唯一一個
個元素,求證:一定存在唯一一個![]() ,使得
,使得![]() 中所有元素的第
中所有元素的第![]() 個坐標分量都是
個坐標分量都是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產的產品![]() 的直徑均位于區間
的直徑均位于區間![]() 內(單位:
內(單位: ![]() ).若生產一件產品
).若生產一件產品![]() 的直徑位于區間
的直徑位于區間![]() 內該廠可獲利分別為10,30,20,10(單位:元),現從該廠生產的產品
內該廠可獲利分別為10,30,20,10(單位:元),現從該廠生產的產品![]() 中隨機抽取200件測量它們的直徑,得到如圖所示的頻率分布直方圖.
中隨機抽取200件測量它們的直徑,得到如圖所示的頻率分布直方圖.
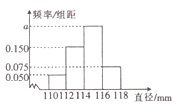
(1)求![]() 的值,并估計該廠生產一件
的值,并估計該廠生產一件![]() 產品的平均利潤;
產品的平均利潤;
(2)現用分層抽樣法從直徑位于區間![]() 內的產品中隨機抽取一個容量為5的樣本,從樣本中隨機抽取兩件產品進行檢測,求兩件產品中至多有一件產品的直徑位于區間
內的產品中隨機抽取一個容量為5的樣本,從樣本中隨機抽取兩件產品進行檢測,求兩件產品中至多有一件產品的直徑位于區間![]() 內的槪率.
內的槪率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分別為AB,AC中點.
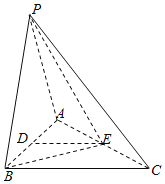
(1)求證:DE∥平面PBC;
(2)求證:AB⊥PE;
(3)求三棱錐P﹣BEC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
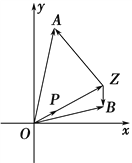
【題目】如圖,已知![]() =(2,1),
=(2,1),![]() =(1,7),
=(1,7),![]() =(5,1),設Z是直線OP上的一動點.
=(5,1),設Z是直線OP上的一動點.
(1)求使![]() 取最小值時的
取最小值時的![]() ;
;
(2)對(1)中求出的點Z,求cos∠AZB的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某校參加高二年級學業水平考試模擬考試的學生中抽取60名學生,將其數學成績分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,畫出如圖的頻率分布直方圖.根據圖形信息,解答下列問題:
(1)估計這次考試成績的眾數,中位數,平均數;
(2)估計這次考試成績的及格率(60分及其以上為及格).

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國在超級計算機方面發展迅速,躋身國際先進水平國家,預報天氣的準確度也大大提高,天氣預報說今后的三天中,每一天下雨的概率都是![]() ,我們可以通過隨機模擬的方法估計概率.我們先產生
,我們可以通過隨機模擬的方法估計概率.我們先產生![]() 組隨機數
組隨機數
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在這組數中,用![]() 表示下雨,
表示下雨,![]() 表示不下雨,那么今后的三天中都下雨的概率近似為( )
表示不下雨,那么今后的三天中都下雨的概率近似為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com