
【題目】已知m,n為兩條不同的直線,![]() ,
,![]() 為兩個(gè)不同的平面,則下列命題中正確的有
為兩個(gè)不同的平面,則下列命題中正確的有![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
A. 0個(gè) B. 1個(gè) C. 2個(gè) D. 3
【答案】B
【解析】
分析:由線面垂直的幾何特征,及線面垂直的第二判定定理,可判斷A的真假;
根據(jù)面面平行的幾何特征及線線位置關(guān)系的定義,可判斷B的真假;
根據(jù)線面垂直及線線垂直的幾何特征,及線面平行的判定方法,可判斷C的真假;
根據(jù)面面平行的判定定理,可以判斷D的真假.
詳解:
由mα,nα,m∥β,n∥β,若a,b相交,則可得α∥β,若a∥b,則α與β可能平行也可能相交,故(1)錯(cuò)誤;
若m∥n,n⊥α根據(jù)線面垂直的第二判定定理可得m⊥α,故(2)正確;
若α∥β,mα,nβ,則m∥n或m,n異面,故(3)錯(cuò)誤;
若m⊥α,m⊥n,則n∥α或nα,故(4)錯(cuò)誤;
故選:B.


 小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個(gè)五位自然數(shù)![]() 數(shù)稱為“跳躍數(shù)”,如果同時(shí)有
數(shù)稱為“跳躍數(shù)”,如果同時(shí)有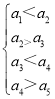 或
或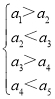 (例如13284,40329都是“跳躍數(shù)”,而12345,54371,94333都不是“跳躍數(shù)”),則由1,2,3,4,5組成沒有重復(fù)數(shù)字且1,4不相鄰的“跳躍數(shù)”共有_____個(gè).
(例如13284,40329都是“跳躍數(shù)”,而12345,54371,94333都不是“跳躍數(shù)”),則由1,2,3,4,5組成沒有重復(fù)數(shù)字且1,4不相鄰的“跳躍數(shù)”共有_____個(gè).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知?jiǎng)狱c(diǎn)P是△PMN的頂點(diǎn),M(﹣2,0),N(2,0),直線PM,PN的斜率之積為﹣![]() .
.
(1)求點(diǎn)P的軌跡E的方程;
(2)設(shè)四邊形ABCD的頂點(diǎn)都在曲線E上,且AB∥CD,直線AB,CD分別過點(diǎn)(﹣1,0),(1,0),求四邊形ABCD的面積為![]() 時(shí),直線AB的方程.
時(shí),直線AB的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() 離心率為
離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點(diǎn)![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點(diǎn),
兩點(diǎn),![]() 為橢圓
為橢圓![]() 的左焦點(diǎn),若
的左焦點(diǎn),若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
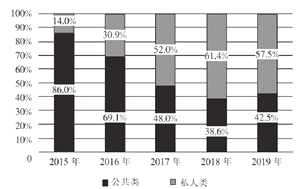
【題目】如圖統(tǒng)計(jì)了截止2019年年底中國(guó)電動(dòng)車充電樁細(xì)分產(chǎn)品占比及保有量情況,關(guān)于這5次統(tǒng)計(jì),下列說法正確的是( )
中國(guó)電動(dòng)車充電樁細(xì)分產(chǎn)品占比情況:
中國(guó)電動(dòng)車充電樁細(xì)分產(chǎn)品保有量情況:(單位:萬臺(tái))
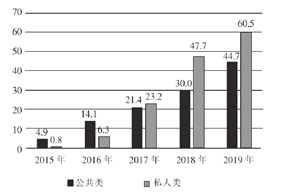
A.私人類電動(dòng)汽車充電樁保有量增長(zhǎng)率最高的年份是2018年
B.公共類電動(dòng)汽車充電樁保有量的中位數(shù)是25.7萬臺(tái)
C.公共類電動(dòng)汽車充電樁保有量的平均數(shù)為23.12萬臺(tái)
D.從2017年開始,我國(guó)私人類電動(dòng)汽車充電樁占比均超過![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】斐波那契數(shù)列(![]() )又稱黃金分割數(shù)列,因數(shù)學(xué)家列昂納多斐波那契(
)又稱黃金分割數(shù)列,因數(shù)學(xué)家列昂納多斐波那契(![]() )以兔子繁殖為例子而引入,故又稱為“兔子數(shù)列”.在數(shù)學(xué)上,斐波納契數(shù)列被以下遞推的方法定義:數(shù)列
)以兔子繁殖為例子而引入,故又稱為“兔子數(shù)列”.在數(shù)學(xué)上,斐波納契數(shù)列被以下遞推的方法定義:數(shù)列![]() 滿足:
滿足:![]() ,
,![]() ,現(xiàn)從數(shù)列的前2024項(xiàng)中隨機(jī)抽取1項(xiàng),能被3整除的概率是( )
,現(xiàn)從數(shù)列的前2024項(xiàng)中隨機(jī)抽取1項(xiàng),能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(Ⅰ)若直線![]() 且曲線
且曲線![]() 在A處的切線與
在A處的切線與![]() 在B處的切線相互平行,求a的取值范圍;
在B處的切線相互平行,求a的取值范圍;
(Ⅱ)設(shè)![]() 在其定義域內(nèi)有兩個(gè)不同的極值點(diǎn)
在其定義域內(nèi)有兩個(gè)不同的極值點(diǎn)![]() 且
且![]() 若不等式
若不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() 上兩點(diǎn),過點(diǎn)
上兩點(diǎn),過點(diǎn)![]() 且斜率為
且斜率為![]() 的兩條直線與橢圓
的兩條直線與橢圓![]() 的交點(diǎn)分別為
的交點(diǎn)分別為![]() .
.
(Ⅰ)求橢圓![]() 的方程及離心率;
的方程及離心率;
(Ⅱ)若四邊形![]() 為平行四邊形,求
為平行四邊形,求![]() 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com