
ȫ �� �� �{(di��o) ��
��(sh��)�W(xu��)ԇ�}��һ��
ע��1.��������150�֣���ԇ�r(sh��)�g120��犣�
2. ��ԇ�������߿���ԇ��VҎ(gu��)���Ŀ�ԇ��(n��i)�ݡ�

�ڢ�����x���} ��60�֣�
һ��
�x���}:�����}��12С�}��ÿС�}5�֣���60�֡���ÿС�}�o�����Ă�(g��)�x�(xi��ng)�У�ֻ��һ�(xi��ng)�Ƿ����}ĿҪ��ġ�
1.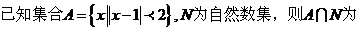

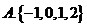
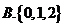
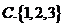
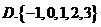

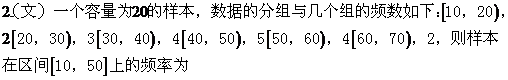


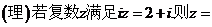

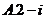
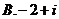
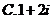
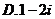


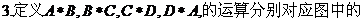 �٢ڢۢܣ���ô�D�еĢݢ�����(du��)��(y��ng)���\(y��n)��Y(ji��)��������
�٢ڢۢܣ���ô�D�еĢݢ�����(du��)��(y��ng)���\(y��n)��Y(ji��)��������





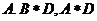
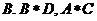

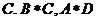
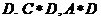

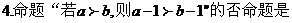

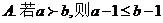
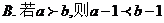

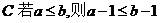
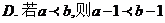



A. 1
B
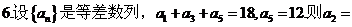

A. 2
B
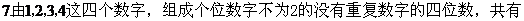

A 8��(g��) B.9��(g��)
C.18��(g��) D.19��(g��)
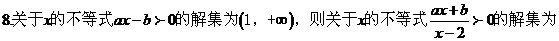

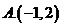
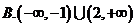

C.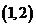
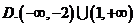

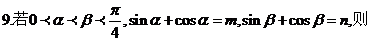

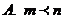
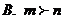
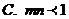
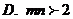


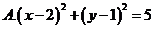
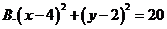

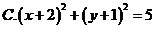
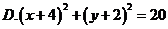

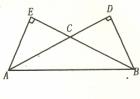
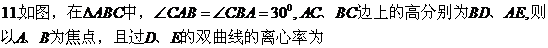

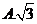
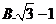

 D.2
D.2
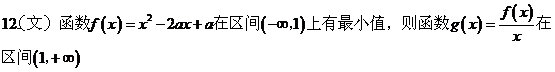 A. ����Сֵ
B. �����ֵ C. �ǜp����(sh��)
D. ��������(sh��)
A. ����Сֵ
B. �����ֵ C. �ǜp����(sh��)
D. ��������(sh��)
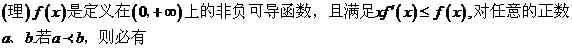
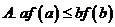
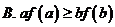

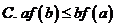
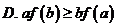


�}̖(h��o)
1
2
3
4
5
6
7
8
9
10
11
12
��


�ڢ��(���x���} ��90��)
����
����}�������}��4С�}��ÿС�}5�֣���20�֣��Ѵ������}�ЙM���ϡ�


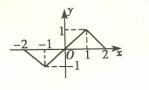
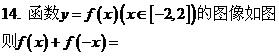

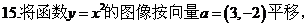

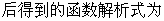

16.���Ѓɂ�(g��)���}���Ƿ���Ҫ�ڡ� ���ϼ�һ��(g��)�l����Y(ji��)Փ���ܘ�(g��u)������?�����Ҫ��Ո(q��ng)?zh��)��һ��(g��)����(y��ng)�ėl�����������Ҫ���t�ڡ� ���τ���/��
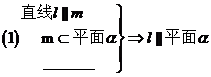

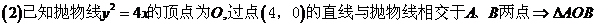
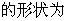


����
����}�������}��6С�}����70�֡����(y��ng)���������f�����C���^�̻����㲽�E��
17.����С�}�M��10�֣�
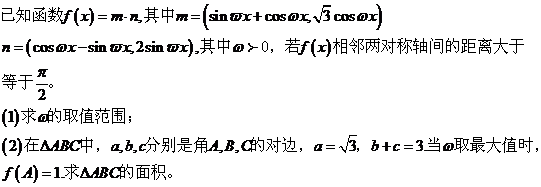



18. ����С�}�M��12�֣�
�����r(sh��)�g
��1��
�������˸������3�Σ�������c����t��ǡ�ÃɴΓ���9�h(hu��n)�ĸ����Ă�(g��)�Y(ji��)���Է�?j��n)?sh��)����ʽ��ʾ����
��2��
�������˸������3�Σ������tÿ�ζ�����9�h(hu��n)���ϵĸ��ʣ��Y(ji��)��һ��?j��n)?sh��)����ʽ��ʾ��
��������3���O(sh��)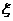 �鏈������@�ΛQِ�Г��еĭh(hu��n)��(sh��)����
�鏈������@�ΛQِ�Г��еĭh(hu��n)��(sh��)����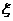 ��������
��������







19. ����С�}�M��12�֣�
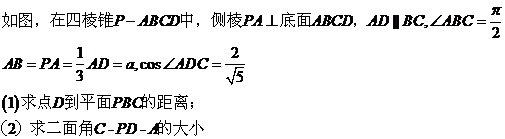

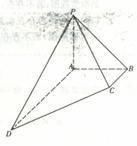








20. ����С�}�M��12�֣�
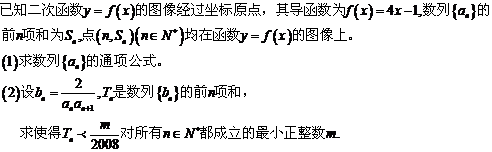





21. ����С�}�M��12�֣�
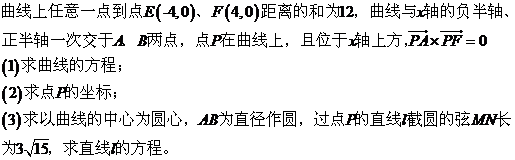









22. ����С�}�M��12�֣�
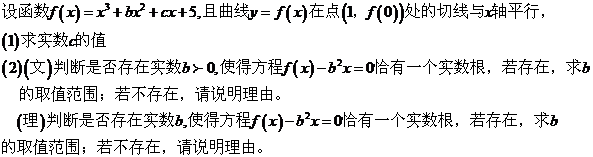
�{(di��o)�У�һ����(sh��)�W(xu��)��
1.B
2.(��)B �ӱ��څ^(q��)�g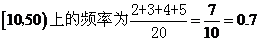
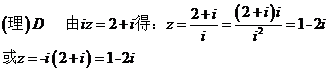
3.B
4��C
5��B 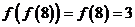
6��C. 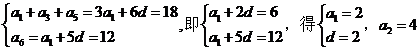
7��C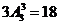
8��B.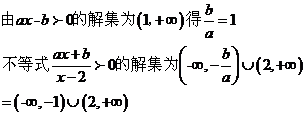
9��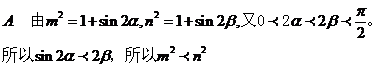
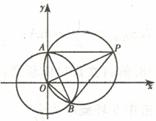 10��A
��D��
10��A
��D��
�A����OP���c(di��n)��2��1����
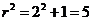 ��
��
��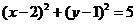 ��
��
11��C �O(sh��)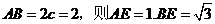 ��
��
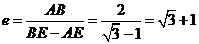 ��
��
12�����ģ�D �ɺ���(sh��)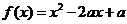 �څ^(q��)�g
�څ^(q��)�g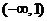 ������Сֵ���t
������Сֵ���t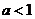 ��
��
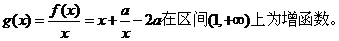
(��) 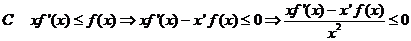 ��
��
��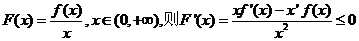 ��
��
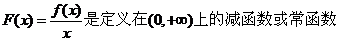 ��
��
������(sh��)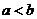 ���t����
���t����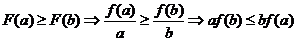 ��
��
13��20
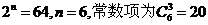 ��
��
14��0
15��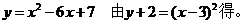
16����1��
17����: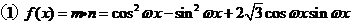
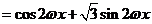
 ����������������������������������������������3��
����������������������������������������������3��
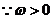 ��
��
 ��
��
���}���֪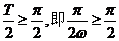 ��
��
���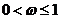 ��
��
��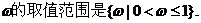 ����������������������������5��
����������������������������5��
(2)��(1)��֪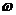 �����ֵ��1,
�����ֵ��1,
 ��
��
 ��
��
��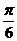
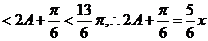 ��
��
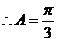 ��������������������������������������������8��
��������������������������������������������8��
�����Ҷ���֪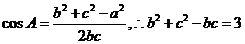 ��
��
��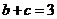 ,(li��n)�����
,(li��n)�����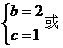
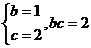 ��
��
18����:(��)(1)���}��:��������һ��,����10�h(hu��n)�ĸ��ʞ�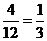 ��
��
����9�h(hu��n)���ʞ�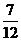 ��
��
�����������ǡ�ÃɴΓ���9�h(hu��n)�ĸ��ʞ�: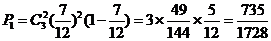 ��
��
ͬ��,�a(b��)���tǡ�ÃɴΓ���9�h(hu��n)�ĸ��ʞ�: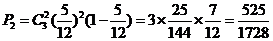 ��
��
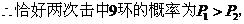
��������9�h(hu��n)�ĸ����^��; ������������������������������������������������6��
(2)����tÿ�ζ�����9�h(hu��n)���ϵĸ���;
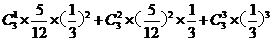
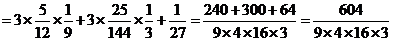
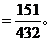
����tÿ�ζ�����9�h(hu��n)���ϵĸ��ʞ� ��������������������������������12�� ��10��
��������������������������������12�� ��10��
(��)(3)
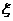
10
9
8
7
P
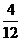
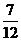
0
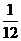
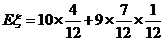
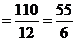 ������������������������������������������������12��
������������������������������������������������12��
19���ⷨһ����1����D���������F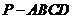 �У�
�У�
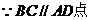
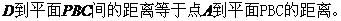
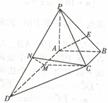
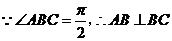 ��
��
��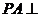 ����
����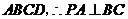 ��
��
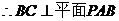 ��������������������������������3��
��������������������������������3��
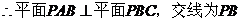 ��
��
�^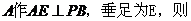
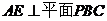 ��
��
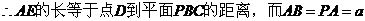 ��
��
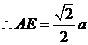 ��
��
���c(di��n)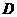 ��ƽ��
��ƽ�� ��������������������������������6��
��������������������������������6��
��2��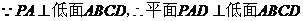
��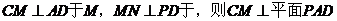 ��
��
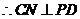 ��
��
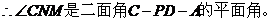 ������������������������9��
������������������������9��

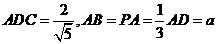 ��
��
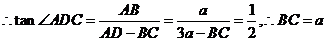 ��
��
��֪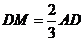 ��
��
��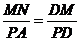 ��
��
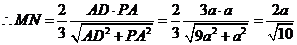 ��
��
 ��
��
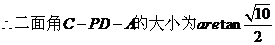 ������������������������12��
������������������������12��
�ⷨ������D��A��ԭ�c(di��n)���քe��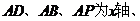
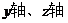 ���������gֱ=������(bi��o)ϵ��
���������gֱ=������(bi��o)ϵ��
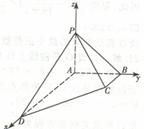 ��1��
��1��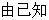
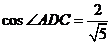 ��
��
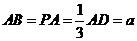 ��
��
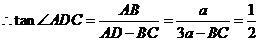 ��
��
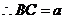
�t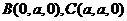 ��
��
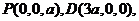 ����������������������������4��
����������������������������4��
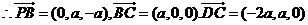 ��
��
�O(sh��)ƽ��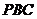 ��һ��(g��)��������
��һ��(g��)��������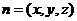 ��
��
�t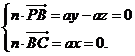 ��
��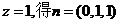 ��
��
�t�c(di��n)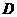 ��ƽ��
��ƽ��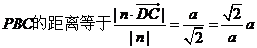 ����������������7��
����������������7��
��2��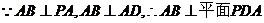 ��
��
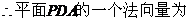
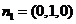 ��
��
�O(sh��)ƽ��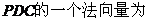
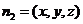 ��
��
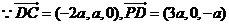 ��
��
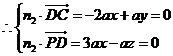
��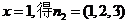 ����������������������������������10��
����������������������������������10��
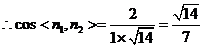 ��
��

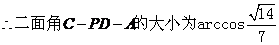 ��������������������12��
��������������������12��
20.�⣺��1����֪���κ���(sh��)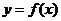 �ĈD��(j��ng)�^����(bi��o)ԭ�c(di��n)��
�ĈD��(j��ng)�^����(bi��o)ԭ�c(di��n)��
�O(sh��)�@�����(sh��)��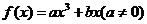 ��
��
�t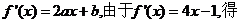
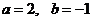 ��
��
����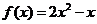 ����������������������������������3��
����������������������������������3��
����?y��n)��c(di��n)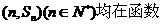
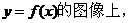
����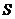
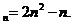
��(d��ng)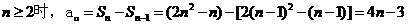 ��
��
��(d��ng)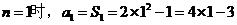 ��
��
���ԣ�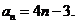 ����������������������������6��
����������������������������6��
��2���ɣ�1����֪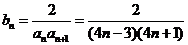
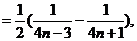 ��������������������������������9��
��������������������������������9��
��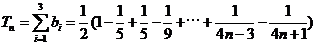
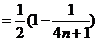 ��
��
��ˣ�Ҫʹ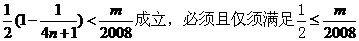 ��
��
��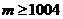 ��
��
���ԝM��Ҫ�����С������(sh��)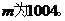 ����������������������12��
����������������������12��
21.�⣺��1���O(sh��)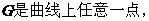
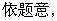
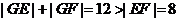 ��
��
������������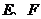 �齹�c(di��n)�ęE�A��
�齹�c(di��n)�ęE�A��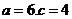 ��
��
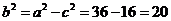 ��
��
��������ęE�A���̞�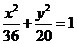 ������������������������������������3��
������������������������������������3��
��2������֪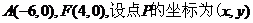 ��
��
�t
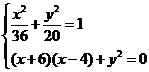
�t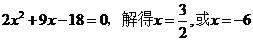 ��
��
����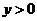 ������ֻ��ȡ
������ֻ��ȡ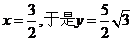 ��
��
�����c(di��n)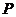 ������(bi��o)��(
������(bi��o)��(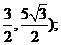 ����������������������������6��
����������������������������6��
��3���A�Ğ飨0��0�����돽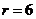
�A���̞�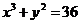 ��
��
���^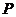 ��ֱ��
��ֱ��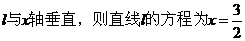 ��
��
�@�r(sh��)���A�ĵ�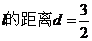 ��
��
����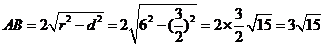 ��
��
�����}�⣻����������������������������9��
���^
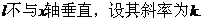
�tֱ��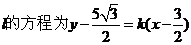 ��
��
��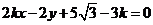 ��
��
�@�r(sh��)���A�ĵ�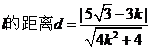 ��
��
����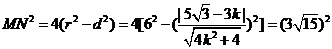 ��
��
�����ã�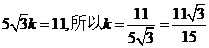 ��
��
����ֱ��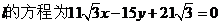 ��
��
�C�ϣ������ֱ��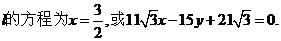 ����12��
����12��
22.�⣺��1��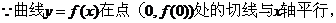
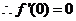
��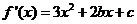 ��
��
�t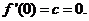 ..............3��
..............3��
��2�����ģ���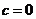 ������
������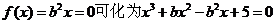 ��
��
���O(sh��)���ڌ�(sh��)��(sh��) 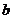 ʹ�ô˷���ǡ��һ��(g��)��(sh��)��(sh��)����
ʹ�ô˷���ǡ��һ��(g��)��(sh��)��(sh��)����
�t��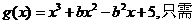
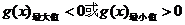 ��
��
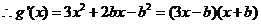 ��............6��
��............6��
��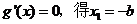 ��
��
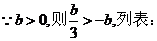
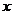
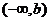
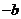
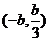
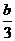
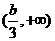
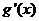
+
0
�D
0
+
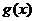
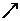
�O��ֵ
�OСֵ
����������������������������������������������������9��
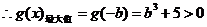
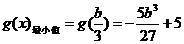 ��
��
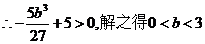 ��
��
��(sh��)��(sh��)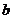 ��ȡֵ�����ǣ�0��3��������������������������������������12��
��ȡֵ�����ǣ�0��3��������������������������������������12��
��������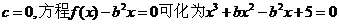 ��
��
���O(sh��)���ڌ�(sh��)��(sh��)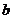 ʹ�ô˷���ǡ��һ��(g��)��(sh��)��(sh��)����
ʹ�ô˷���ǡ��һ��(g��)��(sh��)��(sh��)����
�t��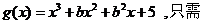
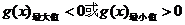 ��
��
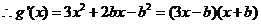 ��������������������5��
��������������������5��
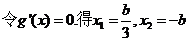 ��
��
����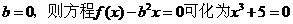 ��
��
�˷���ǡ��һ��(g��)��(sh��)��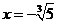 ��
��
����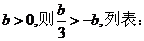
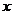
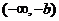
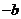
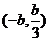
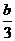
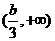
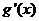
+
0
�D
0
+
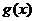
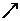
�O��ֵ
�OСֵ

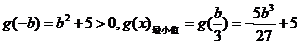 ��
��
 ��������������������������9��
��������������������������9��
����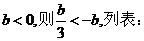
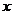
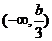
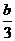

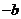
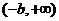
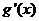
+
0
�D
0
+
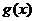
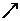
�O��ֵ
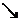
�OСֵ
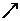
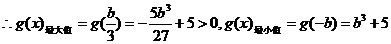 ��
��
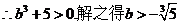 ��
��
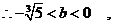
�C�Ϣ٢ڢۿɵã���(sh��)��(sh��)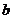 ��ȡֵ������
��ȡֵ������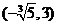 ��������������12��
��������������12��
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com