
合肥市2009年高三第二次教學質量檢測
數學試題(文)
(考試時間:120分鐘 滿分:150分)
注意事項:
1.選擇題用答題卡的考生,答第I卷前,考生務必將自己的姓名、準考證號、試題科目用2B鉛筆涂寫在答題卡上。
2.選擇題用答題卡的考生,在答第I卷時,每小題選出答案后,用2B鉛筆把答題卡上對應題目的答案標號涂黑,如需改動,用橡皮擦干凈后,再選涂其他答案,不能答在試題卷和答題卷的選擇題欄中;不用答題卡的考生,在答第I卷時,每小題選出答案后,填在答題卷相應的選擇題欄上。
3.答第Ⅱ卷時,考生務必將自己的學校、姓名、考點、準考證號填在答題卷相應的位置;答題時,請用0.5毫米的黑色簽字筆直接答在答題卷上,不要在試題卷上答題。
4.考試結束,監考人將答題卷和答題卡一并收回,第I、Ⅱ卷不收回。
參考數據公式:
①獨立性檢驗臨界值表

0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
②獨立性檢驗隨即變量 值計算公式:
值計算公式:


第I卷(滿分60分)
一、選擇題(本大題共有12個小題,每小題5分,共60分;在每小題給出的四個選項中,只有一項是符合題目要求的)
1.復數 在復平面上所對應的點位于
在復平面上所對應的點位于
A.第一象限 B.第二象限 C.第三象限
D.第四象限
2.已知集合啊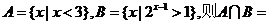

A.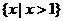 B.
B.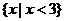 C.
C.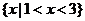 D.
D.

3.下列命題錯誤的是
A.命題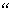 若
若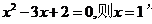 的逆否命題為“若
的逆否命題為“若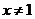 ,則
,則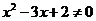 ”
”
B.若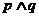 為假命題,則
為假命題,則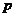 ,
,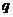 均為假命題
均為假命題
C.對于命題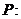 存在
存在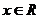 ,使得
,使得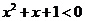 ,則
,則 為:任意
為:任意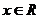 ,均有
,均有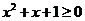

D.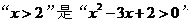 的充分不必要條件
的充分不必要條件
4.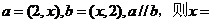

A.2
B.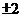 D.1
D.1
5.十進制數147化為四進制數為
A.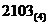 B.
B. C.
C.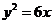 D.
D.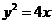

6.直線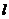 過拋物線
過拋物線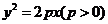 的焦點,且與拋物線交于A、B兩點,若線段AB的長是
的焦點,且與拋物線交于A、B兩點,若線段AB的長是
8,AB的中點到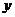 軸的距離是2,則比拋物線方程是
軸的距離是2,則比拋物線方程是
A.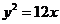 B.
B.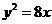 C.
C.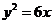 D.
D.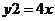

7.在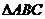 中,角
中,角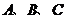 所對的邊分別為
所對的邊分別為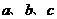 ,且
,且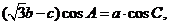 則
則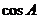 的值等于
的值等于
A.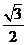 B.
B.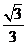 C.
C.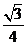 D.
D.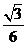

8.函數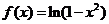 的圖象只可能是
的圖象只可能是
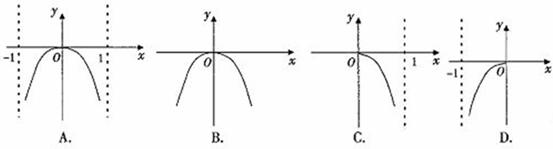

9.已知函數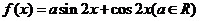 圖象的一條對稱軸方程為
圖象的一條對稱軸方程為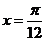 ,則
,則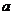 的值為
的值為
 A.
A.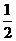 B.
B.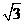 C.
C.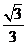 D.2
D.2 
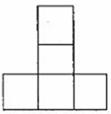
10.用若干個棱個為1的正方體搭成一個幾何體,其正視圖、側視圖都是
如右圖形,對這個幾何體,下列說法正確的是
A.這個幾何體的體積一定是7
B.這個幾何體的體積一定是10
C.這個幾何體的體積的最小值是6,最大值是10
D.這個幾何體的體積的最小值是7,最大值是11
11.已知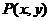 是函數
是函數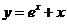 的圖象上的點,則點
的圖象上的點,則點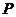 到直線
到直線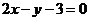 的最小距離為
的最小距離為
A.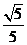 B.
B.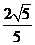 C.
C.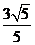 D.
D.

12.設函數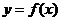 滿足
滿足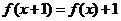 ,則函數
,則函數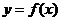 與
與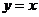 圖象叫點的個數可能是
圖象叫點的個數可能是
A.無窮多個 B.0個或者有限個 C.有限個 D.0個或者無窮多個




 第Ⅱ卷(滿分90分)
第Ⅱ卷(滿分90分)
二、填空題(本大題共4小題,每小題4分,共16分)
13.已知橢圓的中心在原點,焦點在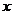 軸上,離心率為
軸上,離心率為
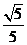 ,且過
,且過 ,則橢圓的方程為________;
,則橢圓的方程為________;
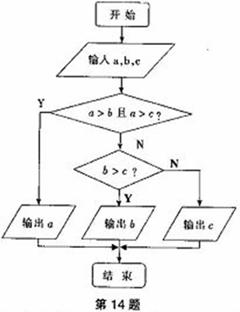
若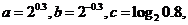 則輸出的數是______;
則輸出的數是______;
15.已知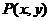 滿足約束條件
滿足約束條件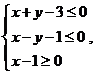

則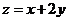 的最大值是___________________;
的最大值是___________________;

16.某企業職工的月工資數統計如下:
月工資數(元)
10000
8000
5500
2500
1600
1200
900
600
500
得此工資人數
1
3
3
8
20
35
45
3
2
經計算,該企業職工工資的平均值為1565元,中位數是_____元,眾數是_______元;
如何選取該企業的月工資代表數呢?企業法人主張用平均值,職工代表主張用眾數,監管部門主張用中位數;
請你站在其中一立場說明理由:______________________________________________。



三、解答題(本大題共6小題,共74分;解答應寫出文字說明、證明過程或演算步驟)
17.(本小題滿分12分)已知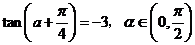 。
。
(1)求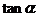 的值;
的值;
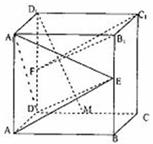 (2)求
(2)求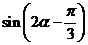 的值。
的值。
18.(本小題滿分12分)
在正方體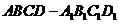 中,
中,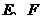 分別為棱
分別為棱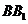 和
和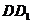 中點。
中點。
(1)求證:平面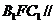 平面
平面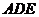 ;
;
(2)試在棱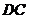 上求一點
上求一點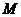 ,使
,使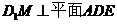



19.(本小題滿分12分)
在平面直角坐標系中, ,其中
,其中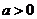 且
且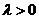 ,求動點
,求動點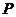 的軌跡方程,并說明軌跡的類型
的軌跡方程,并說明軌跡的類型


20.(本小題滿分12分)
某學校課題組為了研究學生的數學成績與物理成績之間的關系,隨即抽取高二年紀20名學生某次考試成績(百分制)如下表所示:
序號
1
2
3
4
5
6
7
8
9
10
數學成績
95
75
80
94
92
65
67
84
98
71
物理成績
90
63
72
87
91
71
58
82
93
81

序號
11
12
13
14
15
16
17
18
19
20
數學成績
67
93
64
78
77
90
57
83
72
83
物理成績
77
82
48
85
69
91
61
84
78
86
若數學成績90分(含90分)以上為優秀,物理成績85分(含85分)以上為優秀。
(1)根據上表完成下面的2×2列聯表:

數學成績優秀
數學成績不優秀
合計
物理成績優秀
物理成績不優秀
12
合計
20
(2)根據題(1)中表格的數據計算,有多少的把握,認為學生的數學成績與物理成績之間有關系?
(3)若按下面的方法從這個20個人中抽取1人來了解有關情況:將一個標有數字1,2,3,4,5,6的正六面體骰子連續投擲兩次,記朝上的兩個數字的乘積為被抽取人的序號,試求:
①抽到12號的概率;②抽到“無效序號(序號大于20)”的概率。
21.(本小題滿分12分)
已知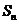 為正項數列
為正項數列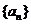 的前
的前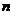 項和,且滿足
項和,且滿足 。
。
(1)求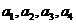 ;、
;、
(2)求數列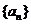 的通項公式;
的通項公式;
(3)若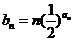 ,數列
,數列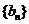 的前
的前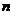 項和為
項和為 ,試比較
,試比較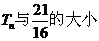


22.(本小題滿分14分)
已知函數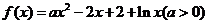

(1)若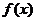 在其定義域上是單調增函數,求實數
在其定義域上是單調增函數,求實數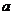 的取值集合;
的取值集合;
(2)當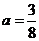 時,函數
時,函數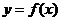 在
在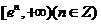 有零點,求
有零點,求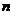 的最大值
的最大值




湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com